Question

Задайте формулой линейную функцию графиком которой служит прямая проходящая через точку А(2;3) и параллельна графику функции у=1,5х-3. Постройте её график

Answer 1

Ответ:

Линейная функция имеет вид y = kx + b.

Графики линейных функций параллельны, если их угловые коэффициенты равны. Т.е. графики функций y₁ = k₁x + b₁  и y₂ = k₂x + b₂  параллельны, если k₁ = k₂ ,  (b₁ ≠ b₂).

Линейная функция имеет угловой коэффициент k = 1,5.

Так как график линейной функции проходит через точку (2; 3), то при x = 2 значение y = 3. Найдем число b.

3 = 1,5 * 2 + b; 3 = 3 + b;  b = 3 - 3; b = 0.

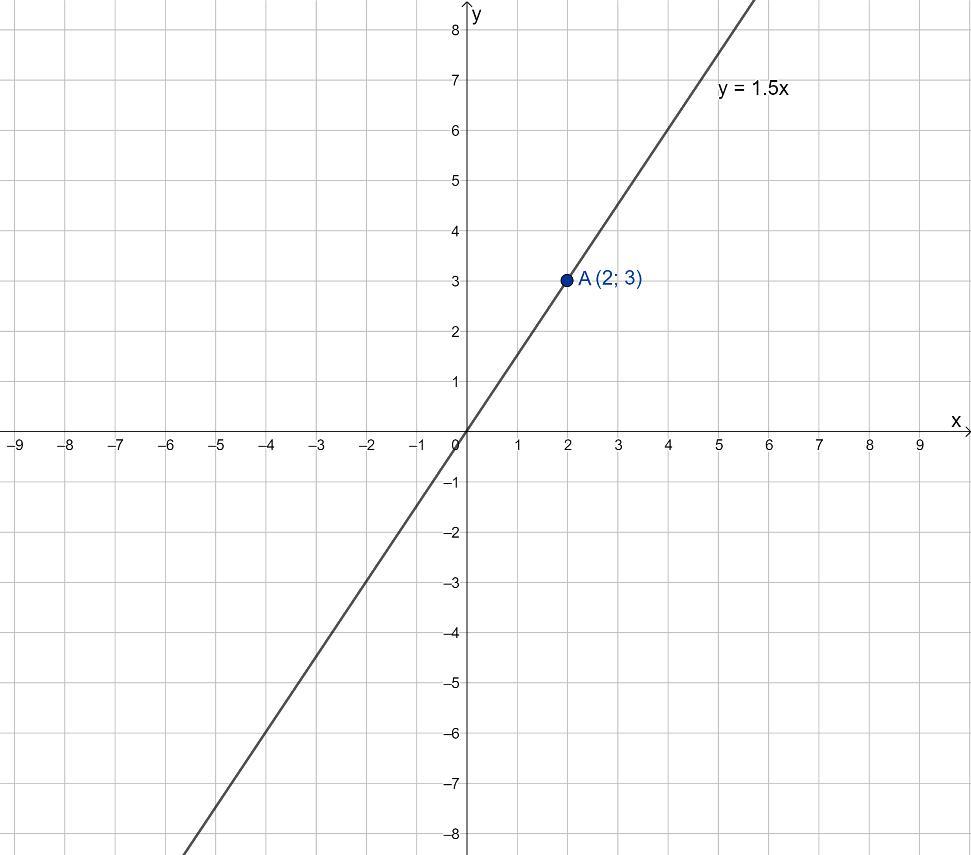
Линейная функции имеет вид y = 1,5x. Ее график в приложении.

Answer 2

Ответ:

Объяснение:

Уравнение прямой:

y = k·x + b

Для функции

y = 1,5·x -3

k = 1,5

Тогда:

y₀ = k·x₀ + b₀

Координаты точки A:

x₀ = 2

y₀ = 3

Имеем:

3 = 1,5·2 + b₀

b₀ = 0

Искомая функция

y = 1,5·x

Строим графики: