Задание:
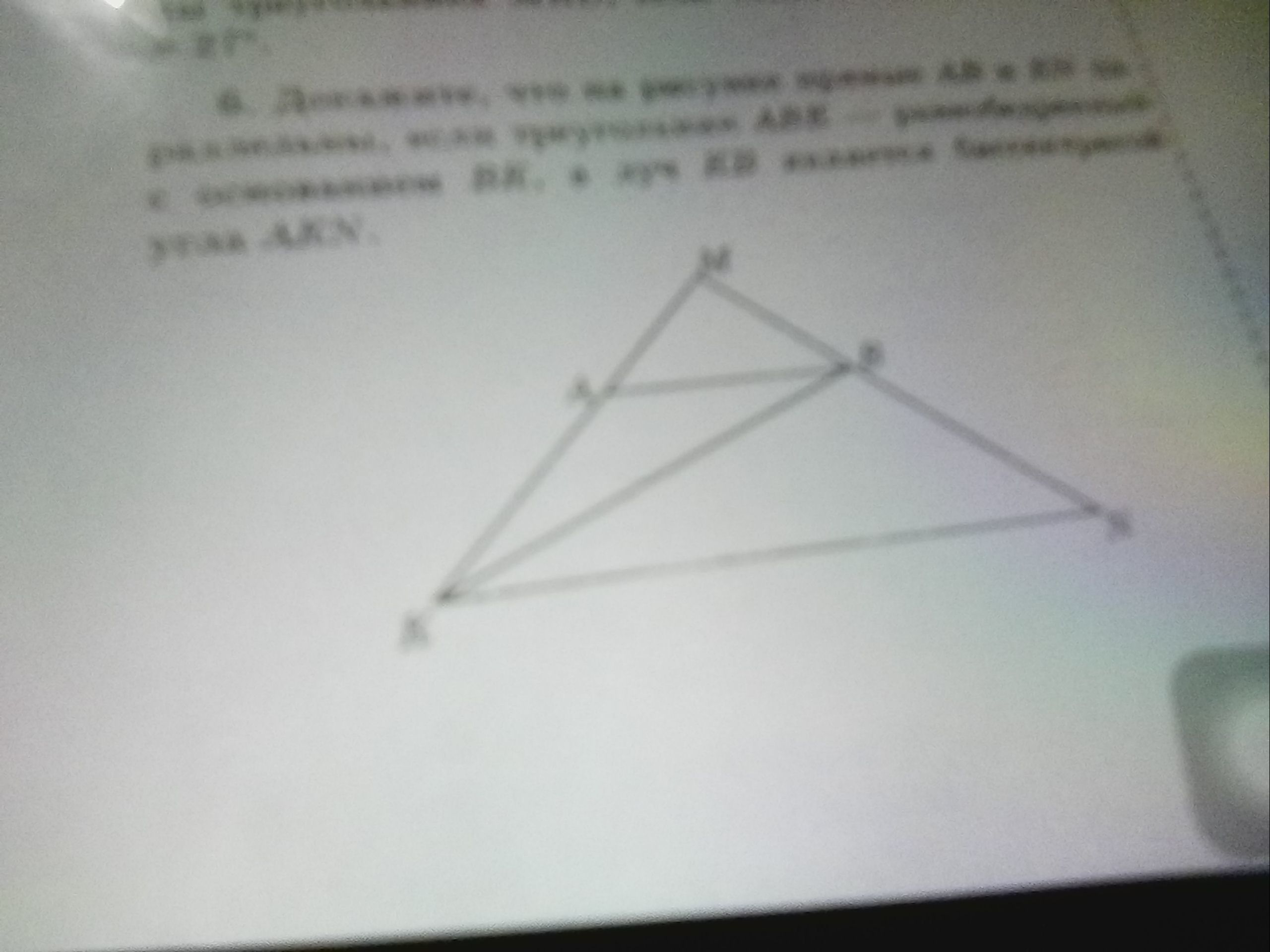
Докажите что на рисунке прямые AB и KN параллельны, если треугольник ABK-равнобедренный с основанием BK, а луч KB является бессектрисой угла AKN.
(Даю 35баллов)
Срочно!
Приложения:
Ответы на вопрос
Ответил aay0303
0
В равнобедренном треугольнике КАВ углы при основании равны. А поскольку КВ является биссектрисой угла К, то она делит угол пополам. Через тоску В проведём прямую паралельно стороне КМ и обозначим P точку её пересечения со стороной КN/. Углы АКВ и PBK равны как внутренние накрест лежащие между параллельными AK и РК и секущей КВ. Треугольники КВР и КВА равны, так как основание КВ общее и углы при основании равны. Следовательно в четырёхугольнике ABPK противоположные углы равны, противоположные стороны равны и параллельны. Что и требовалось доказать.
Новые вопросы