Question

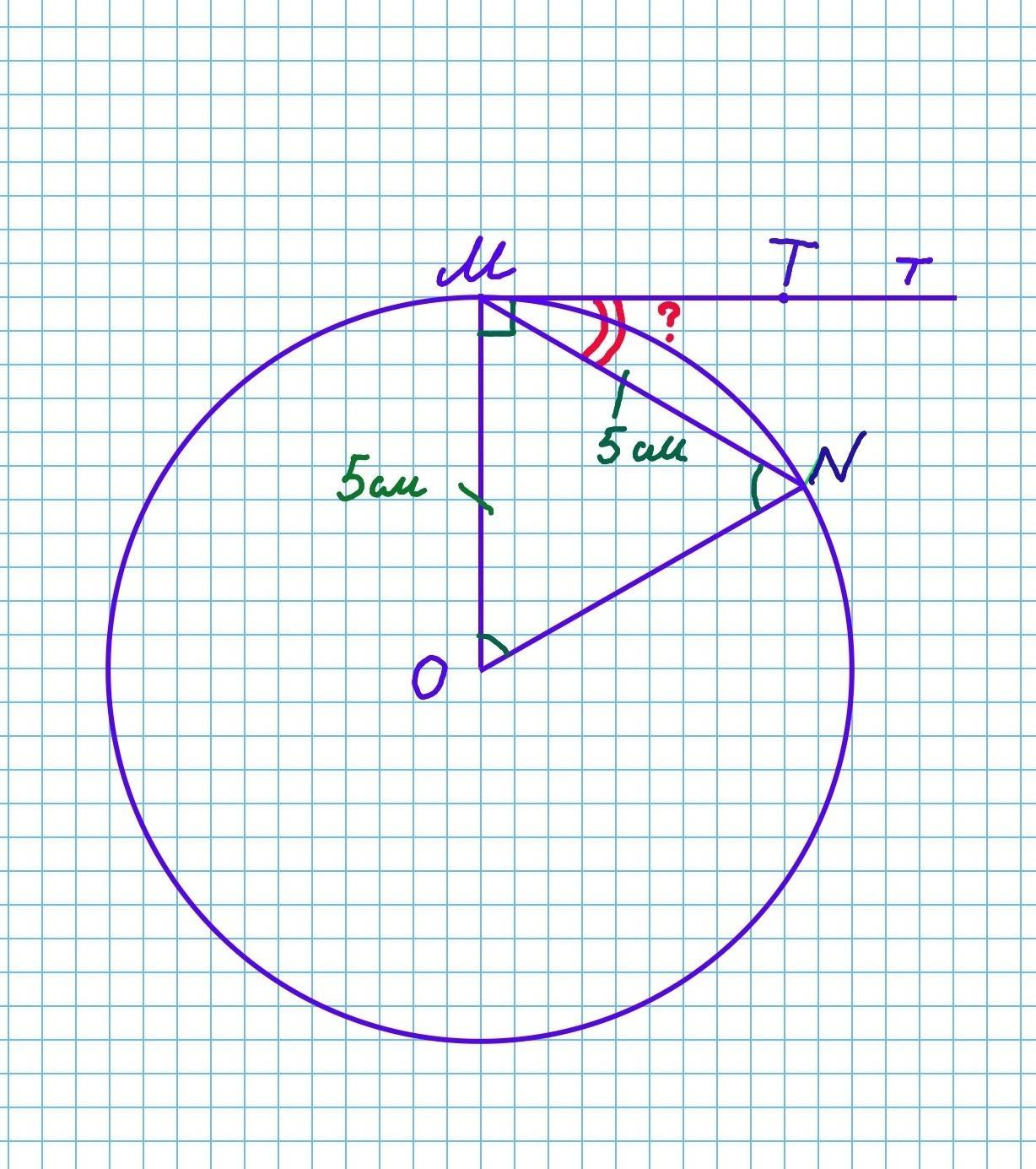
Взаимное расположение прямой и окружности Через точку М окружности проведена хорда MN и прямая т, имеющая с данной окружностью только одну общую точку. Растояние от центра окружности до прямой т равно 5 см. Найди угол между данной прямой и хордой, если хорда MN равна радиусу. Ответ:​

Answer 1

Ответ:

Угол между прямой т и хордой MN равен 30°

Объяснение:

Через точку М окружности проведена хорда MN и прямая т, имеющая с данной окружностью только одну общую точку. То есть прямая т является касательной к окружности.

• Касательная к окружности - это прямая, имеющая с ней только одну общую точку.

Расстояние от центра окружности до прямой т равно 5 см.

• Касательная к окружности перпендикулярна радиусу, проведённому в точку касания: OM⟂MT. ∠OMT=90°.

То есть радиус МО является расстоянием от центра окружности до прямой т.

R=OM=MN=5см.

Найдём угол между прямой т и хордой MN.

Рассмотрим треугольник MON.

Так как OM=MN=ON=R, то △MON - равносторонний.

В равностороннем треугольнике все углы равны.

=> ∠OMN =180°÷3=60°.

∠NMT=∠OMT-∠OMN=90°-60°=30°.

Ответ: Угол между прямой т и хордой MN равен 30°