Высота проведеная из вершины прямого угла прямоугольного треугольника равна 6см и делит гипотенузу на отрезки один из которых больше другого на 5см.Найдите стороны треугольника
Ответы на вопрос
Ответил Trover
1
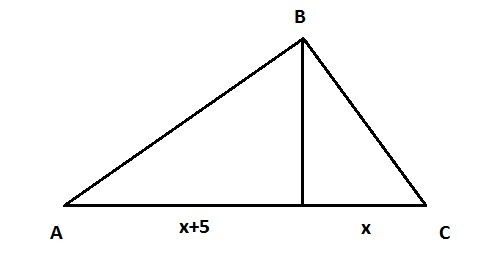
(см. рис.)
Один отрезок гипотенузы x см, второй (x+5) см. Тогда по т. Пифагора катеты:
AB² = 36+(x+5)²
BC² = 36+x²
Из треугольника ABC гипотенуза AC:
AC² = AB²+BC²
(2x+5)² = 36+(x+5)²+36+x²
4x²+20x+25 = x²+x²+10x+25+72
2x²+10x-72 = 0 ÷2
x²+5x-36 = 0
D = 25+4*36 = 169
x1 = 4
x2 = -9 - не подходит по смыслу.
Тогда
AB = √(36+(x+5)²) = √(36+81) = √(117) = 3√(13)
BC= √(36+9) = √(45) = 3√5
AC = √(5+8) = √(13)
Один отрезок гипотенузы x см, второй (x+5) см. Тогда по т. Пифагора катеты:
AB² = 36+(x+5)²
BC² = 36+x²
Из треугольника ABC гипотенуза AC:
AC² = AB²+BC²
(2x+5)² = 36+(x+5)²+36+x²
4x²+20x+25 = x²+x²+10x+25+72
2x²+10x-72 = 0 ÷2
x²+5x-36 = 0
D = 25+4*36 = 169
x1 = 4
x2 = -9 - не подходит по смыслу.
Тогда
AB = √(36+(x+5)²) = √(36+81) = √(117) = 3√(13)
BC= √(36+9) = √(45) = 3√5
AC = √(5+8) = √(13)
Приложения:
Новые вопросы