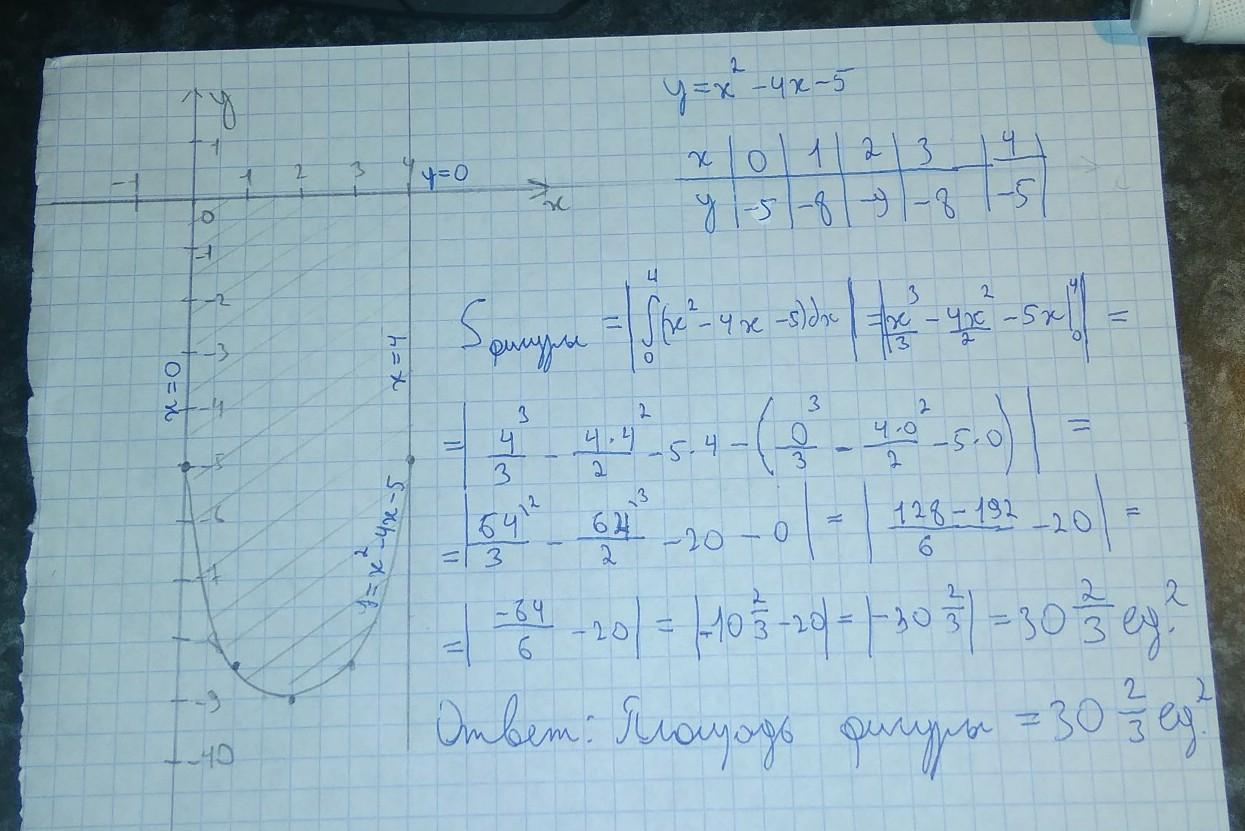
Вычислите с помощью определенного интеграла площадь фигуры, ограниченной линиями. у=х^2-4х-5 , у=0, х=0,х=4 с рисунком.
dimauchenik654454:
С рисунком?
да, с рисунком
Ок
Ответы на вопрос
Ответил dimauchenik654454
1
Ответ:
30 2/3 ед.²
Объяснение:
Решение на фотографии.
Приложения:
Ответил NNNLLL54
0
Приложения:

Новые вопросы