Question

Вычислите координаты точек пересечения параболы y=1/5x^2 и прямой y=20-3x

Answer 1

Пошаговое объяснение:

Приравниваем и получаем квадратное уравнение.

1/5*x² = 20 - 3*x

y = 0,2*x²+3*x+-20 - квадратное уравнение.

a*x² + b*x + c = 0  Вычисляем дискриминант - D.

D = b² - 4*a*c = 3² - 4*(0,2)*(-20) = 25 - дискриминант. √D = 5.

Вычисляем корни уравнения.

x₁ = (-b+√D)/(2*a) = (-3+5)/(2*0,2) = 2/0,4 = 5 - первый корень

x₂ = (-b-√D)/(2*a) = (-3-5)/(2*0,2) = -8/0,4 = -20 - второй корень

5 и -20 - корни уравнения.

Вычисляем ординаты точек пересечения.

y(5) = 20 - 3*5 = 5 и  y(-20) = 20 - 3*(-20) = 80.

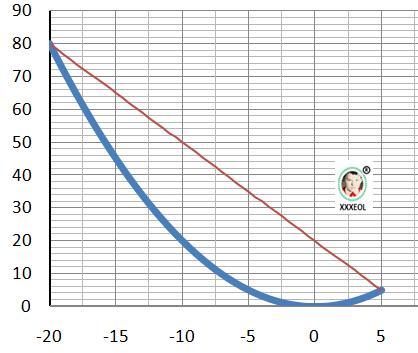
ОТВЕТ:  (-20;80) и (5;5) - точки пересечения.

Рисунок к задаче в приложении.