Вычислить определенный интеграл:
на фото пожалуйста
Приложения:
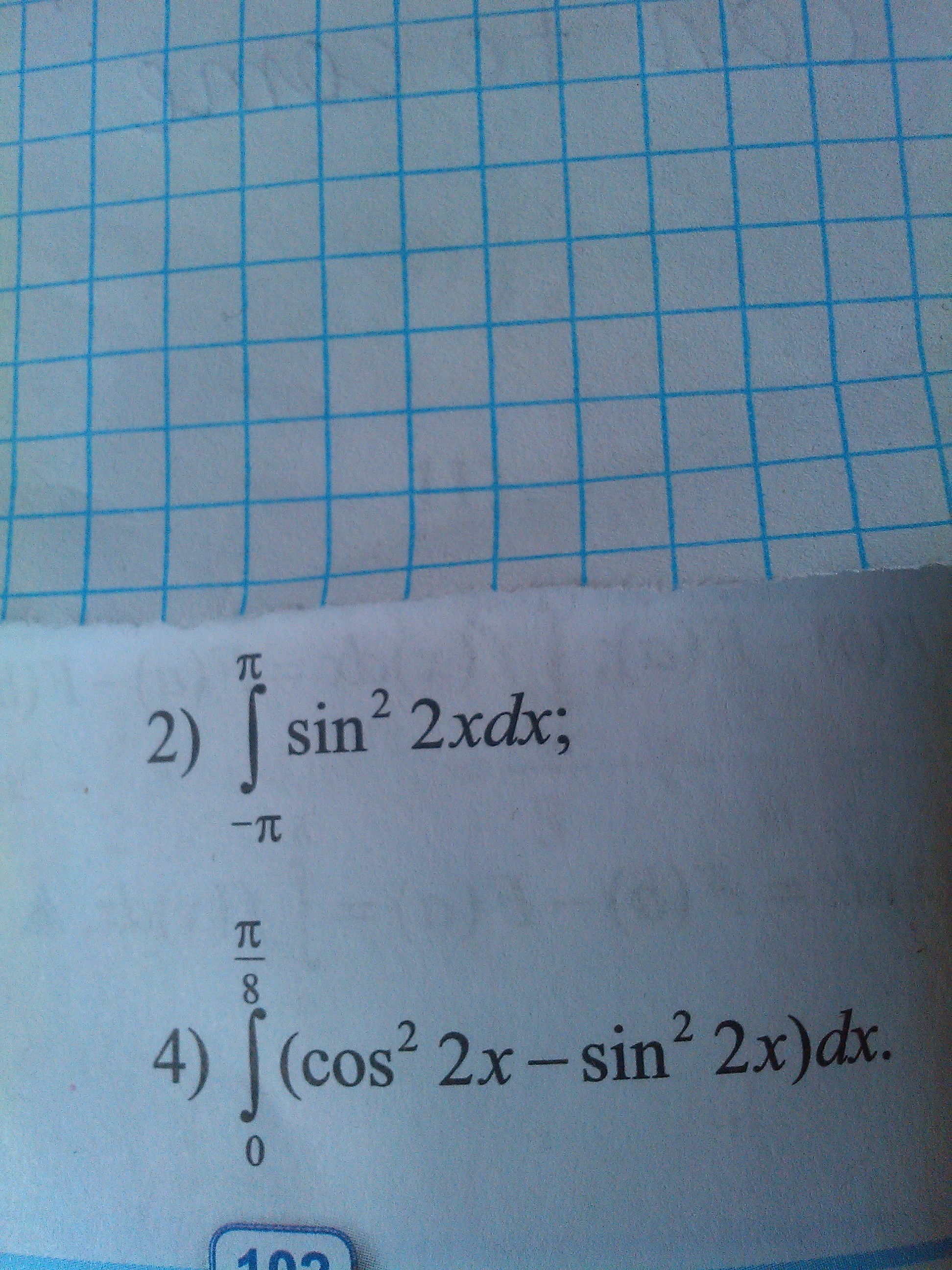
Ответы на вопрос
Ответил Minsk00
0
2) Ответ:
Решение
При вычисление интеграла применяем формулу половинного угла
4) Ответ:
Решение
При вычислении интеграла применяем тригонометрическую формулу двойного угла cos(2x) =cos²(x) - sin²(x)
Новые вопросы