Вычислить:
А) Определенный интеграл от pi/2 до 0 : (3sin 3x - 1/2 cos(x/2))dx
Б) Определенный интеграл от 9 до 0 : 
Приложения:
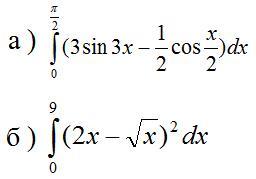
Ответы на вопрос
Ответил aastap7775
1
Новые вопросы
Английский язык,
1 год назад
Алгебра,
1 год назад
Математика,
2 года назад
Алгебра,
2 года назад
Биология,
7 лет назад