Висота прямокутного трикутника, проведена до гіпотенузи, поділяє її на відрізки завдовжки 9 см і 16 см. Знайдіть площу трикутника
Ответы на вопрос
Ответил ReMiDa
1
Ответ:
Площа трикутника дорівнює 150 см²
Объяснение:
Висота прямокутного трикутника, проведена до гіпотенузи, поділяє її на відрізки завдовжки 9 см і 16 см. Знайдіть площу трикутника.
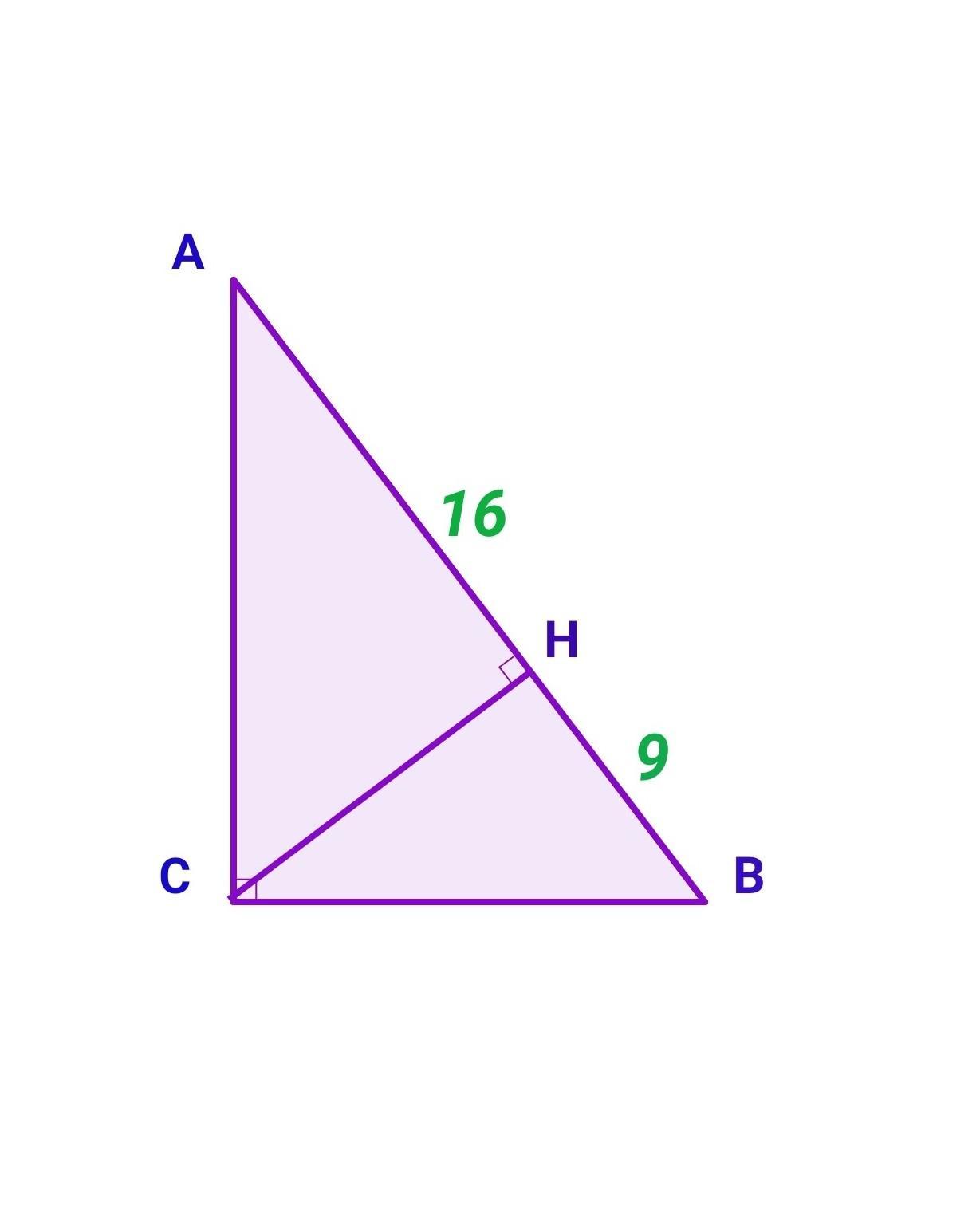
Нехай АВС - даний прямокутний трикутник ∠С=90°, СН⟂АВ, АН=16 см, НВ = 9 см. Знайдемо площу трикутника за формулою:
а - сторона трикутника, - висота, проведена до сторони а.
1) За метричними співвідношеннями у прямокутному трикутнику маємо:
CH²=AH•HB
CH²=16•9=144, CH=12(см)
2) За аксиомою вимірювання відрізків отримаємо: АВ=АН+НВ=16+9=25(см)
3) Площа трикутника АВС:
(см²)
Відповідь: 150 см²
Приложения:
Новые вопросы