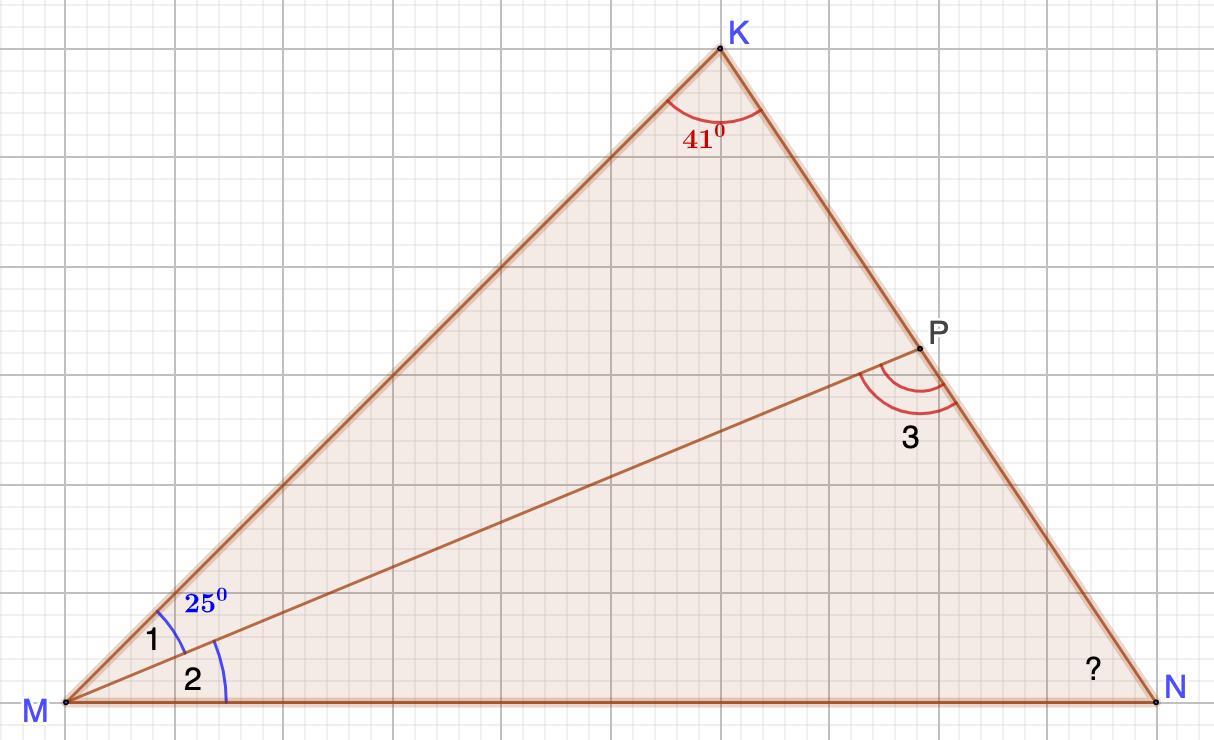
в треугольнике MKN проведена биссектриса MP. угл MKN равен 41°, угол KMP раввин 25°. найди величину MNK. ответы дайте в градусах.
Ответы на вопрос
Ответил natalyabryukhova
1
Ответ:
Величина ∠MNK= 89°
Пошаговое объяснение:
Необходимо найти величину ∠MNK.
Дано: ΔMNK;
MP биссектриса;
∠MKN = 41°, ∠KMP (∠1) = 25°.
Найти: ∠MNK
Решение:
Для того чтобы найти ∠MNK, надо определить два других угла ΔMPN.
1. Рассмотрим ΔMPN.
∠2 = ∠1 = 25° (MP биссектриса)
- Внешний угол треугольника равен сумме углов, не смежных с ним.
⇒ ∠3 = ∠1 + ∠MKN = 25° + 41° = 66°
2. Найдем ∠MNK.
- Сумма углов треугольника равна 180°.
⇒ ∠MNK = 180 - (∠2 + ∠3) = 180° - (25° + 66°) = 180°-91° = 89°
Искомый ∠MNK= 89°
Приложения:
Новые вопросы
Русский язык,
2 года назад
Русский язык,
2 года назад
Биология,
6 лет назад
ОБЖ,
6 лет назад
Математика,
8 лет назад