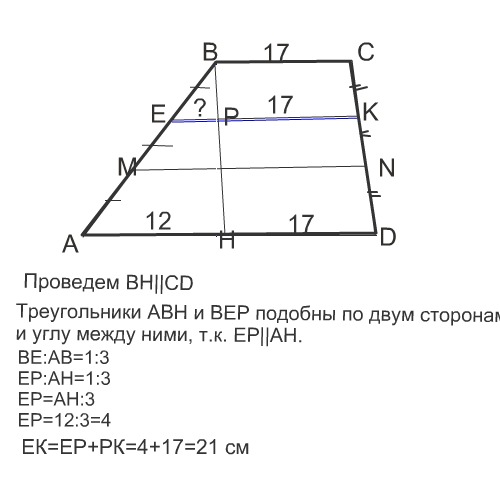
В трапеции АВСD (AD || BC) AD=29 см, BC=17 см. Параллельно основаниям проведены отрезки EK и MN, причем E и M принадлежат стороне AB, а K и N – стороне CD. Найдите EK, если BE=EM=MA.
Ответы на вопрос
Ответил Hrisula
0
Cделаем рисунок к задаче.
Из вершины В опустим на большее основание трапеции отрезок ВН, параллельный стороне CD. Трапеция разделилась на две фигуры: параллелограмм ВСDН и треугольник АВН.
По условию задачи сторона АВ поделена на 3 равных отрезка, ЕК параллельна основанию.
Треугольники АВН и РВЕ подобны.
ВЕ:ВА=1:3 ⇒ЕР:АН=1:3
ЕР:12=1:3
3 ЕР=12
ЕР=4
ЕК=4+17=21 см
Приложения:
Новые вопросы