В трапеции АВCD с основаниями AD = 24 см и ВС = 16 см проведена
Диагональ, которая делит среднюю линию на два отрезка. Сколько
сантиметров составляет меньший из отрезков средней линии?
Ответы на вопрос
Ответил natalyabryukhova
13
Ответ:
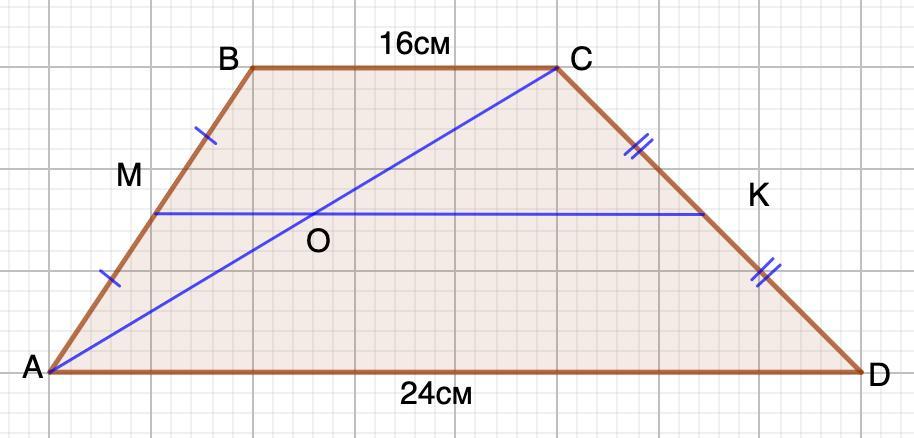
Меньший из отрезков, на которые диагональ трапеции делит среднюю линию равен 8 см.
Объяснение:
Требуется определить меньший из отрезков , на которые делит диагональ среднюю линию трапеции.
Дано: ABCD - трапеция;
МК - средняя линия трапеции;
АС - диагональ;
АС ∩ МК = О;
ВС = 16 см; AD = 24 см.
Найти: Меньший из отрезков МО или ОК.
Решение:
1. Рассмотрим ΔАВС.
- Средняя линия трапеции соединяет середины двух боковых сторон и параллельна основаниям трапеции.
⇒ МК || ВС;
АМ = МВ (условие)
- Признак средней линии треугольника: если отрезок в треугольнике проходит через середину одной из его сторон, пересекает вторую и параллелен третьей — этот отрезок можно назвать средней линией этого треугольника.
⇒ МО - средняя линия ΔАВС.
МО = ВС : 2 = 16 см : 2 = 8 (см)
Получили МО = 8 см.
2. Рассмотрим ΔACD.
ОК || AD
CK = KD
⇒ ОК - средняя линия ΔACD.
ОК = AD : 2 = 24 : 2 = 12 (см)
Получили ОК = 12 см.
Меньший из отрезков, на которые диагональ трапеции делит среднюю линию равен 8 см.
Приложения:
xonkeldievamadina:
да
Новые вопросы
Русский язык,
2 года назад
Английский язык,
2 года назад
Алгебра,
6 лет назад
Математика,
8 лет назад