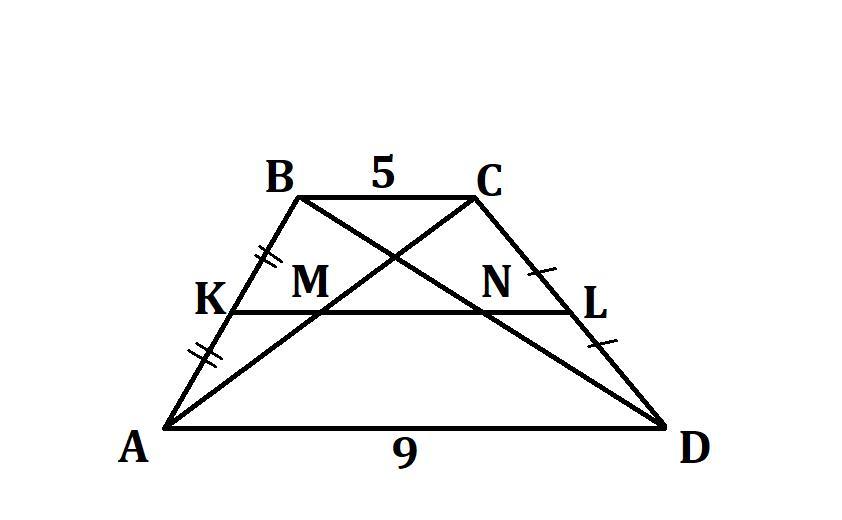
В трапеции ABCD известны основания AD=9 и BC=5. Найдите расстояние между серединами диагоналей трапеции (буквенное обозначение получившегося отрезка - MN).
Ответы на вопрос
Ответил Alyssa08
0
Ответ: MN = 2
Объяснение:
В трапеции ABCD известны основания AD = 9 и BC = 5. Найдите расстояние между серединами диагоналей трапеции (буквенное обозначение получившегося отрезка - MN).
**********
- Средняя линия трапеции проходит через середины диагоналей.
М – середина диагонали АС, N – середина диагонали ВD.
K и L – середины боковых сторон АВ и СD соответственно, то есть KL - средняя линия трапеции ABCD.
⇒ KМ – средняя линия ΔАВС, KM || BC.
⇒ М ∈ KL, поскольку через точку K можно провести на плоскости единственную прямую, параллельную прямой ВС.
KM = 1/2 · BC
Аналогично, N – середина диагонали BD, NL - средняя линия ΔDCB, NL || BC, N ∈ KL.
NL = 1/2 · BC
По свойству средней линии трапеции,
#SPJ3
Приложения:
Новые вопросы