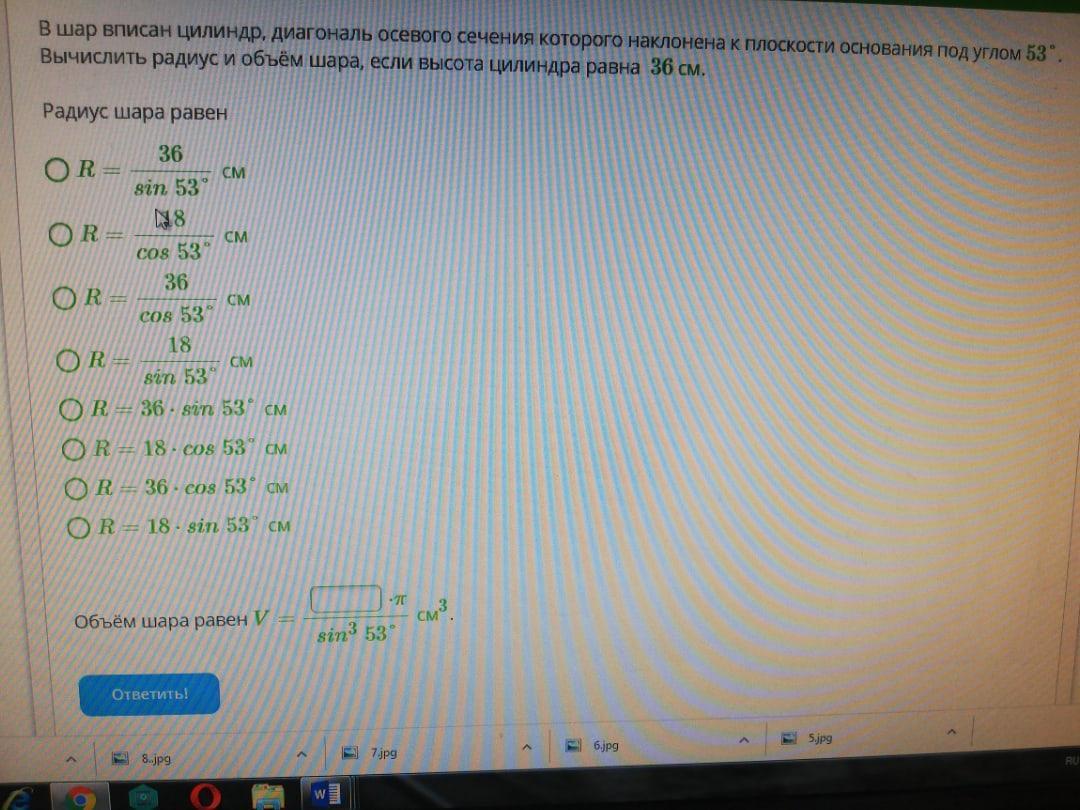
В шар вписан цилиндр, диагональ осевого сечения которого наклонена к плоскости основания под углом 53 градуса.
Вычислить радиус и объём шара, если высота цилиндра равна 36 см.
Приложения:
Ответы на вопрос
Ответил DariosI
0
Ответ:
R=18/sin53 см, V=864/sin³53 см³
Объяснение:
Дано:
∠α=53
h=36 см
Найти:
R -?
V -?
Решение:
Радиус с высотой представляют прямоугольный треугольник с углом 53° и катетом h/2.
sin53°=h/2:R ⇒
R=h/(2sin53°)=36/(2sin53°)=18/sin53° см радиус шара
V=4/3πR³=4/3*(18/sin53)³=864/sin³53 см³ объем шара
Приложения:

Новые вопросы
Английский язык,
2 года назад
Алгебра,
7 лет назад
Литература,
7 лет назад
География,
9 лет назад
Музыка,
9 лет назад