Question

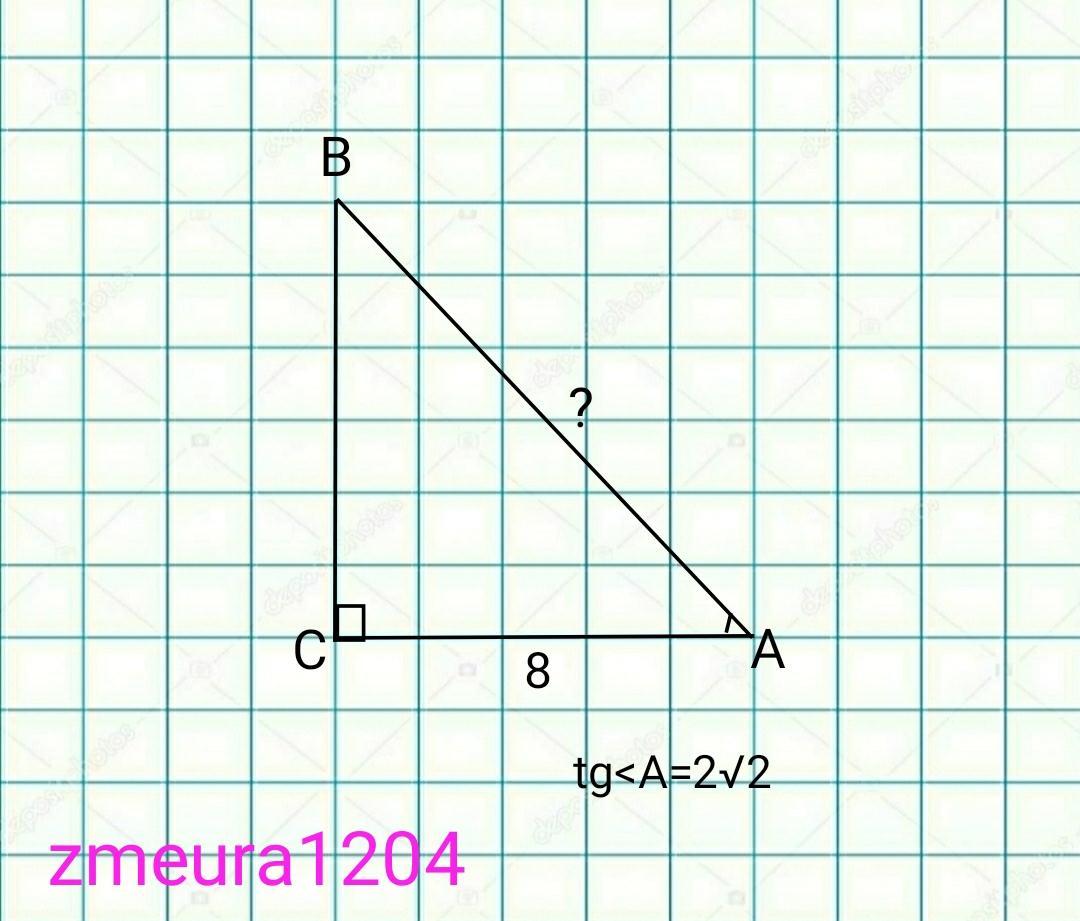
В прямоугольном треугольнике ABC : AC=8 tgBAC=2√2. Найдите длину гипотенузы AB.​

Answer 1

Відповідь:

АВ=24

Пояснення:

tg<A=BC/AC

2√2=BC/8

BС=8*2√2=16√2

Теорема Пифагора

АВ=√(ВС²+АС²)=√(8²+(16√2)²)=√(64+512)=

=√576=24

Answer 2

Ответ:

Гипотенуза AB равна 24 ед..

Объяснение:

Дано:

ΔABC: AB - гипотенуза, <C = 90°

AC = 8 см; tg(<BAC) = 2√2

Найти: AB

Решение:

tg(<BAC) = BC / AC

Подставляем известное: 2√2 = BC / 8  =>  BC = 8 * 2√2 = 16√2

По теореме Пифагора: AB² = AC² + BC²  <=> AB = √(AC² + BC²)

AB = √(8² + (16√2)²) = √(64 + 512) = √576 = 24 (ед.)

Ответ: AB = 24 ед.