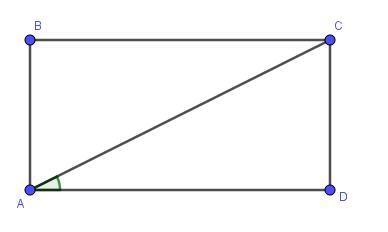
В прямоугольнике периметр равен 2p, а диагональ составляет со стороной угол х. Найдите площадь этого прямоугольника.
Simba2017:
вам понять как я решала задачу и остальные сможете сами решать. А просто списывание готового -пользы не приносит...
время есть у вас сейчас?
Ответы на вопрос
Ответил Аноним
1
Пусть сторона CD = a, тогда . По теореме Пифагора из прямоугольного треугольника ACD
Приложения:
Новые вопросы
Английский язык,
1 год назад
Английский язык,
1 год назад
Алгебра,
1 год назад
Английский язык,
1 год назад
Математика,
6 лет назад
Химия,
6 лет назад