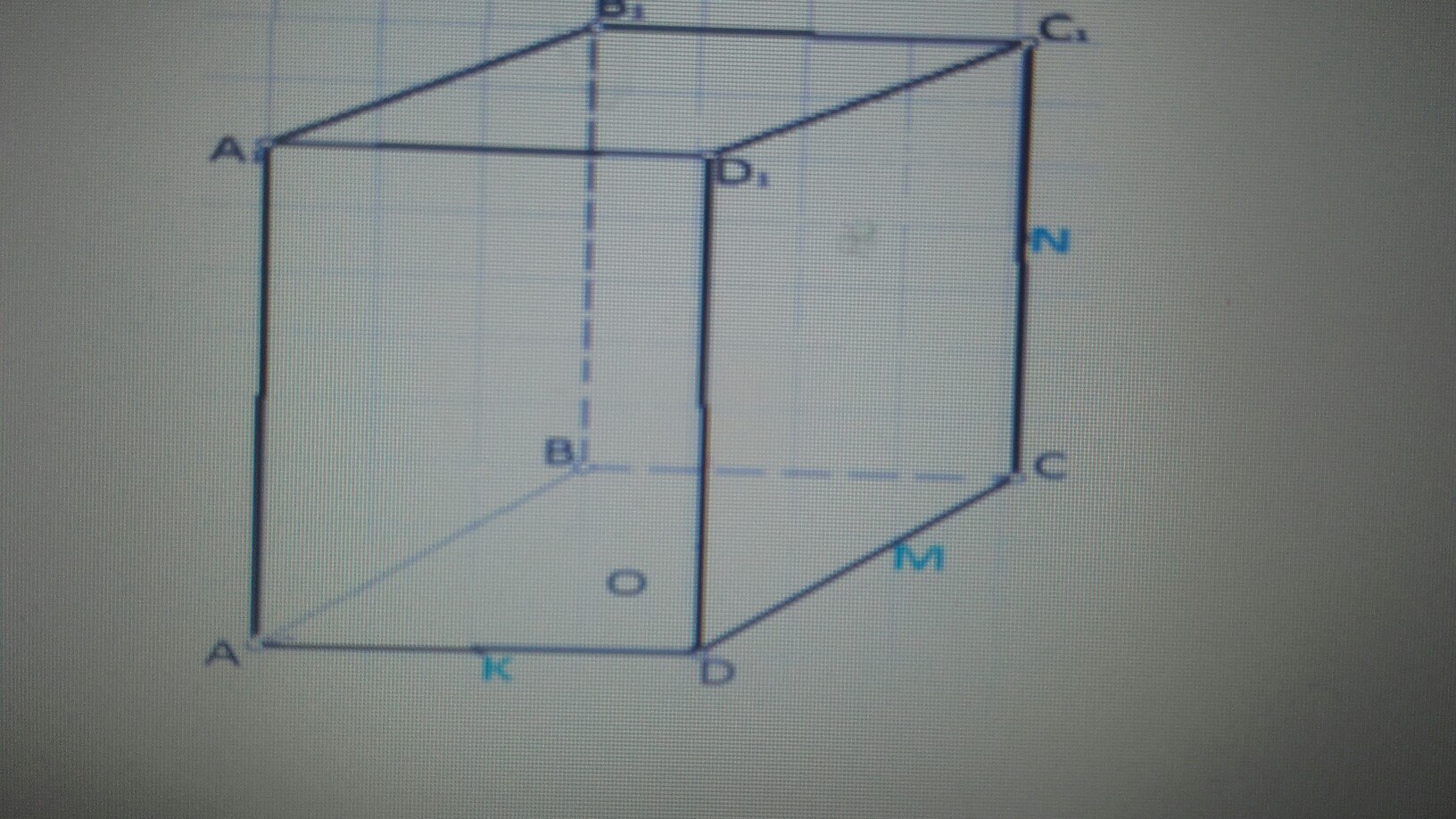
В кубе АВСD
A1 B1 C1 D1 АВ=2 корнь из2 через точки N, M и K проходит сечение. Определите периметр многоугольника, который является сечением, если СN=С1N, DM= MС и АК=КD
Приложения:
Ответы на вопрос
Ответил dnepr1
0
Для получения сечения надо построить 2 дополнительные точки:
- пересечение КМ и ребра ВС,
- пересечение МN и ребра DD1.
Далее проводим отрезки из полученных точек через К и N. В параллельных плоскостях линии сечения параллельны.
В итоге через 6 середин рёбер проходит сечение.
В сечении получаем правильный шестиугольник со стороной а.
а = (2√2/2)*√2 = 2.
Периметр равен Р = 6а = 6*2 = 12.
- пересечение КМ и ребра ВС,
- пересечение МN и ребра DD1.
Далее проводим отрезки из полученных точек через К и N. В параллельных плоскостях линии сечения параллельны.
В итоге через 6 середин рёбер проходит сечение.
В сечении получаем правильный шестиугольник со стороной а.
а = (2√2/2)*√2 = 2.
Периметр равен Р = 6а = 6*2 = 12.
Новые вопросы