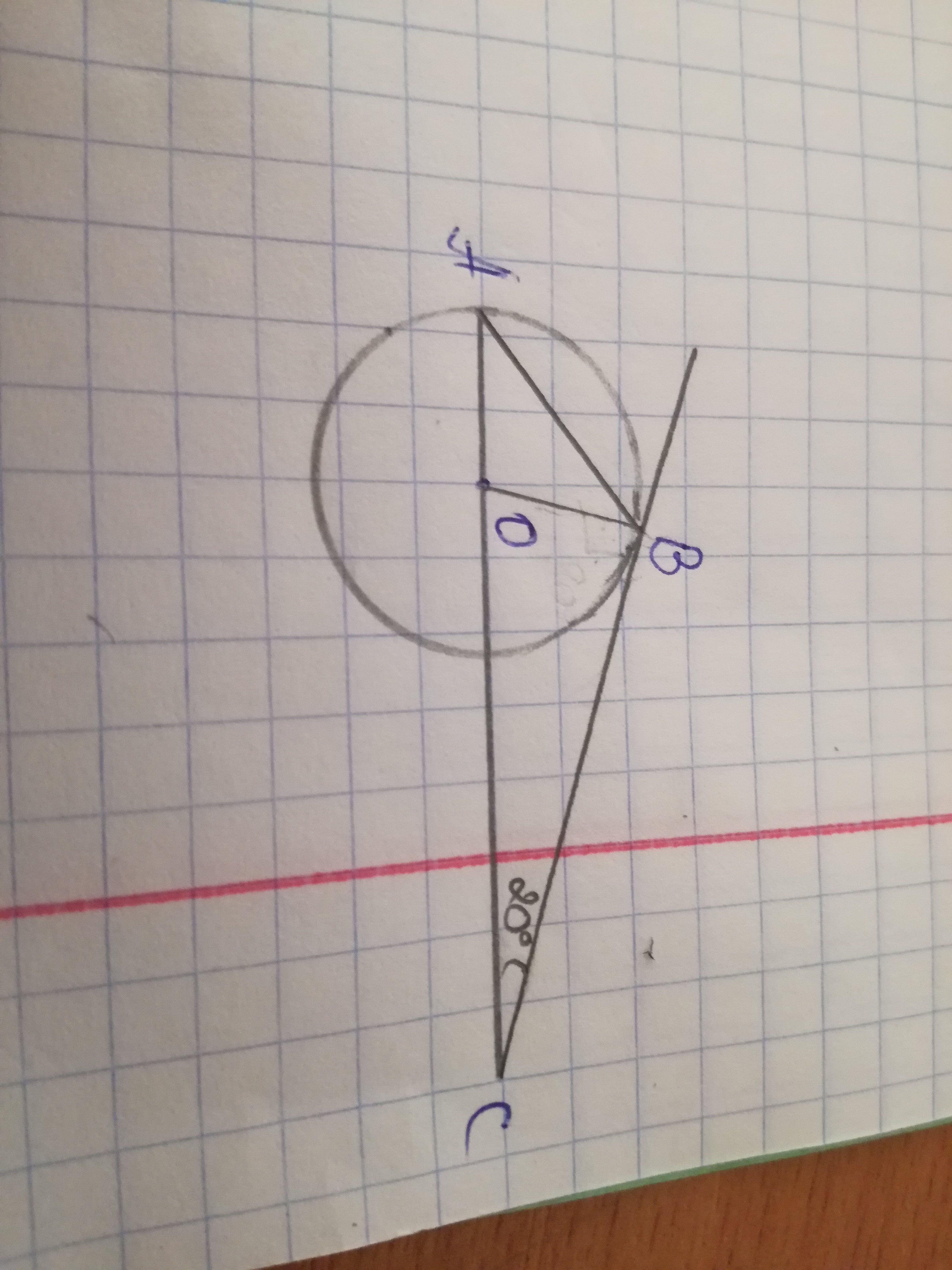
Срочно!
СВ—касательная
угол С=20°
найти Углы треугольника АОВ
Приложения:
Ответы на вопрос
Ответил oxxximironchick
0
смотрите,угол ОВС равен 90°, так как радиус ОВ перпендикулярен касательной СВ
т.к. Угол С=20°
Тогда угол СОВ будет равен 90-29=70°
Если не трудно-пометь ,пожалуйста ,мой ответ,как лучший,буду признательна очень
по рисунку видно, что угол СОВ и угол
ВОА- смежные,а значит их сумма равна 180°
тогда находим угол ВОА ,который равен 180-70=110°
теперь рассматриваем ∆АОВ:
стороны ОА и ОВ в нем равны как радиусы, тогда этот треугольник равнобедренный, а из этого следует ,что углы при его основании равны (углы ОАВ и ОВА)
т.к. сумма углов в треугольнике равна 180°, ТО ПИШЕМ:
УголАОВ+уголАВО+уголОАВ=180°
т.к. угол ОАВ и ОВА равны, то обозначим их за х, а угол АОВ нам известен,он равен 110°, то подставляем и получаем:
2Х+110=180
х=35°
тогда в треугольнике АОВ углы равны:
35° ; 35° ; 110°.
т.к. Угол С=20°
Тогда угол СОВ будет равен 90-29=70°
Если не трудно-пометь ,пожалуйста ,мой ответ,как лучший,буду признательна очень
по рисунку видно, что угол СОВ и угол
ВОА- смежные,а значит их сумма равна 180°
тогда находим угол ВОА ,который равен 180-70=110°
теперь рассматриваем ∆АОВ:
стороны ОА и ОВ в нем равны как радиусы, тогда этот треугольник равнобедренный, а из этого следует ,что углы при его основании равны (углы ОАВ и ОВА)
т.к. сумма углов в треугольнике равна 180°, ТО ПИШЕМ:
УголАОВ+уголАВО+уголОАВ=180°
т.к. угол ОАВ и ОВА равны, то обозначим их за х, а угол АОВ нам известен,он равен 110°, то подставляем и получаем:
2Х+110=180
х=35°
тогда в треугольнике АОВ углы равны:
35° ; 35° ; 110°.
Новые вопросы