!!!СРОЧНО!!!Доказать сходимость числового ряда и найти его сумму
Приложения:
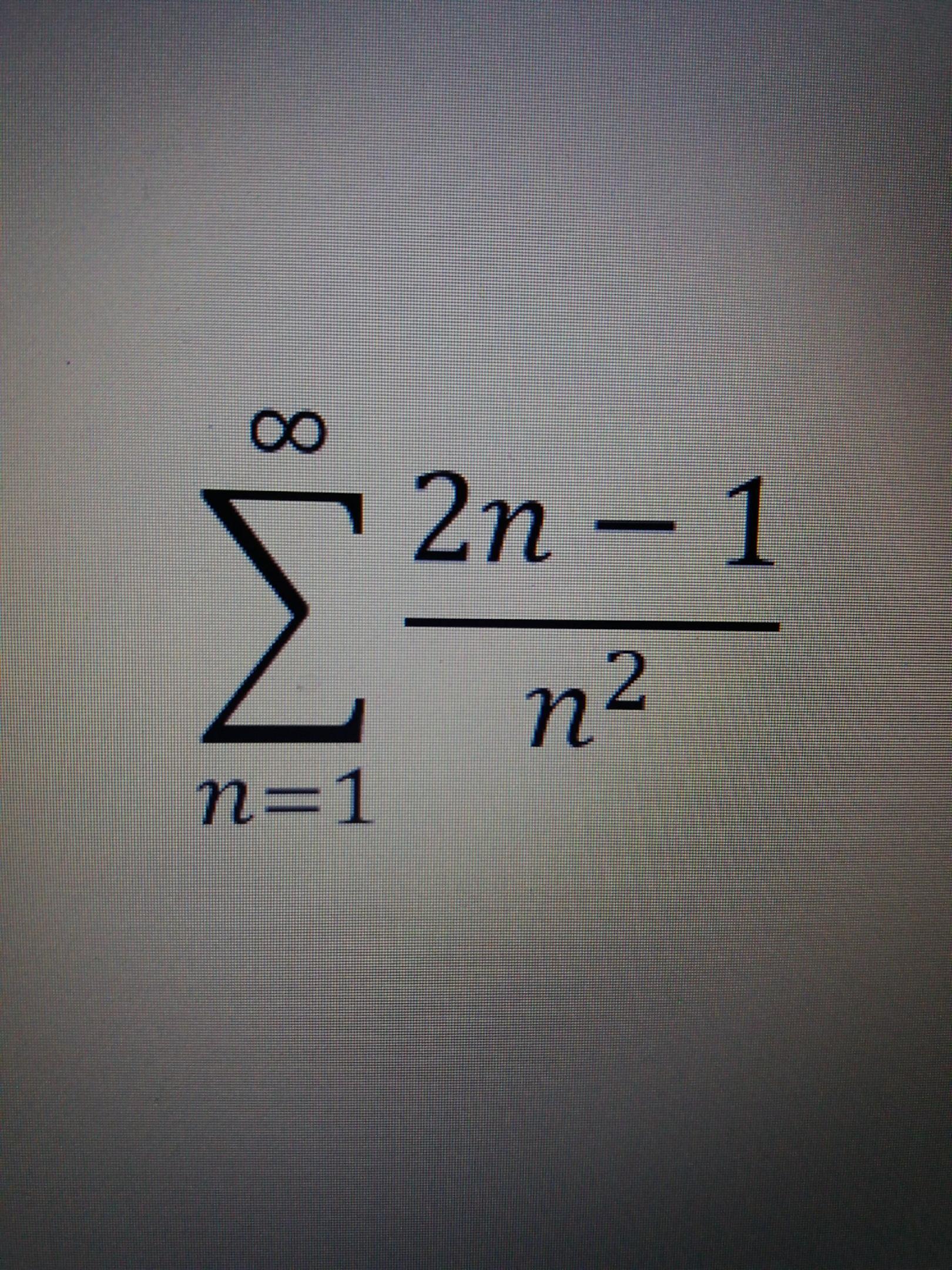

Ответы на вопрос
Ответил igorShap
0
расходится как гармонический,
сходится как обобщенный гармонический с
=> исходный ряд расходится
а значит ряд сходится по радикальному признаку Коши.
Новые вопросы