Решить неопределенный интеграл
Объяснить как внесли корень из икс под знак дифференциала!
Пропишите пожалуйста подробно как вы внесли
Приложения:
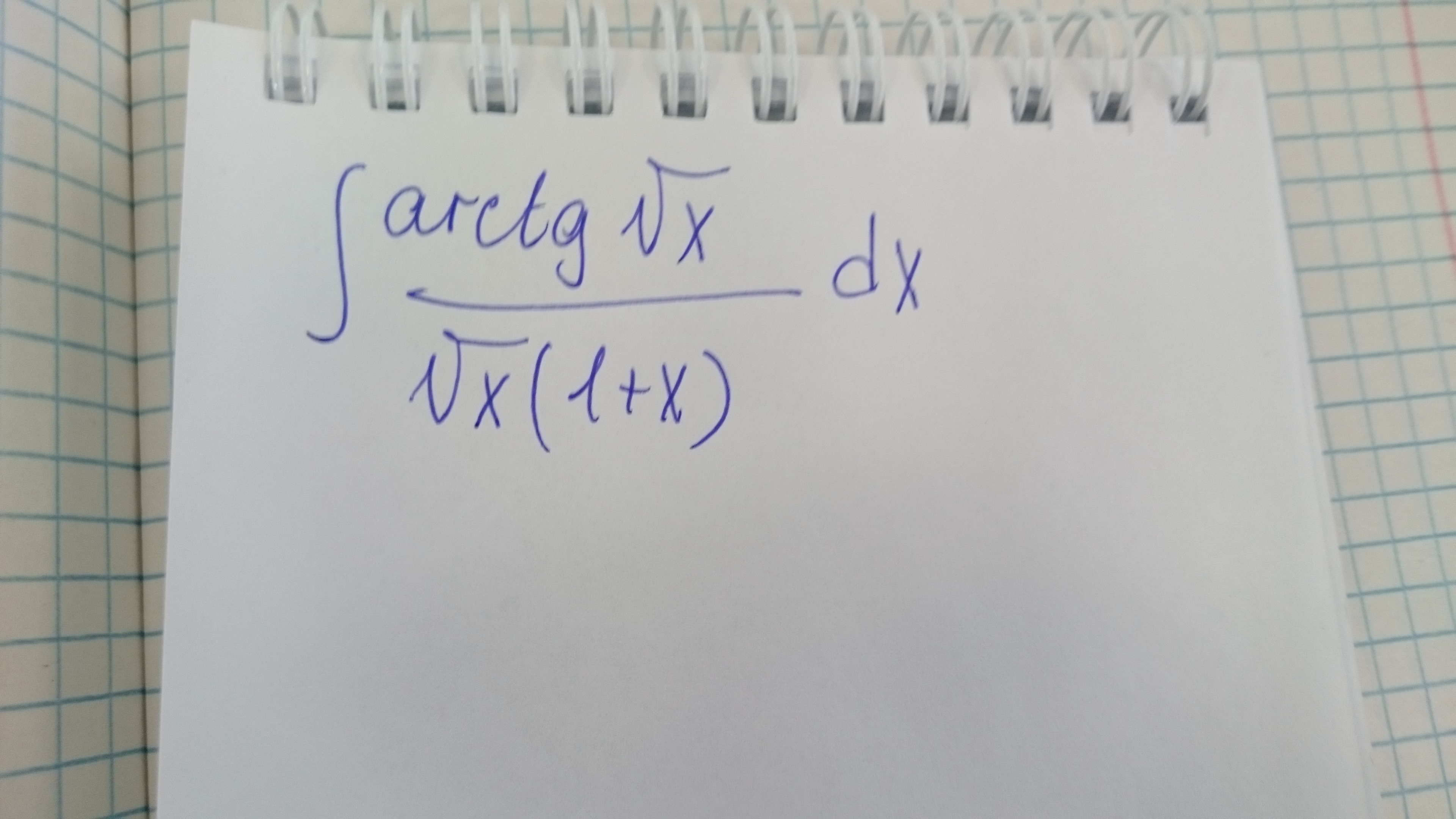
Ответы на вопрос
Ответил HSS9860
0
Рассмотрите такой вариант:
в данном интеграле подводить под знак дифференциала можно дважды: сначала 1/√х, затем выражение 1/(1+х). Первое подведение [dx/√x=2d(√x)], о котором вопрос, алгебраически можно описать так (все обозначения условны, используются для пояснения):
![[ frac{dx}{ sqrt{x}}= 2d( sqrt{x})] d( sqrt{x})=( sqrt{x})'= frac{1}{2 sqrt{x}}; frac{1}{2 sqrt{x}}=2d( sqrt{x}). [ frac{dx}{ sqrt{x}}= 2d( sqrt{x})] d( sqrt{x})=( sqrt{x})'= frac{1}{2 sqrt{x}}; frac{1}{2 sqrt{x}}=2d( sqrt{x}).](https://tex.z-dn.net/?f=%5B+frac%7Bdx%7D%7B+sqrt%7Bx%7D%7D%3D+2d%28+sqrt%7Bx%7D%29%5D++d%28+sqrt%7Bx%7D%29%3D%28+sqrt%7Bx%7D%29%27%3D+frac%7B1%7D%7B2+sqrt%7Bx%7D%7D%3B+++frac%7B1%7D%7B2+sqrt%7Bx%7D%7D%3D2d%28+sqrt%7Bx%7D%29.)
Проще говоря, подведение под знак дифференциала - операция взятия производной, при условии, что будет домножение на коэффициент в целях сохранения равенства.
Таким образом, выложенный интеграл решится примерно так:

в данном интеграле подводить под знак дифференциала можно дважды: сначала 1/√х, затем выражение 1/(1+х). Первое подведение [dx/√x=2d(√x)], о котором вопрос, алгебраически можно описать так (все обозначения условны, используются для пояснения):
Проще говоря, подведение под знак дифференциала - операция взятия производной, при условии, что будет домножение на коэффициент в целях сохранения равенства.
Таким образом, выложенный интеграл решится примерно так:
Ответил Shanon
0
спасибо большое!
Новые вопросы
География,
2 года назад
Математика,
2 года назад
Математика,
8 лет назад
Геометрия,
8 лет назад
Геометрия,
9 лет назад