Пожалуйста решение с рисунками.
1) Сколько ребер, граней, вершин имеет 14-угольная призма?
2) Стороны основания прямоугольного параллелепипеда равны 6 см и 9 см, а диагональ равна 11 см. Найдите площадь полной поверхности параллелепипеда.
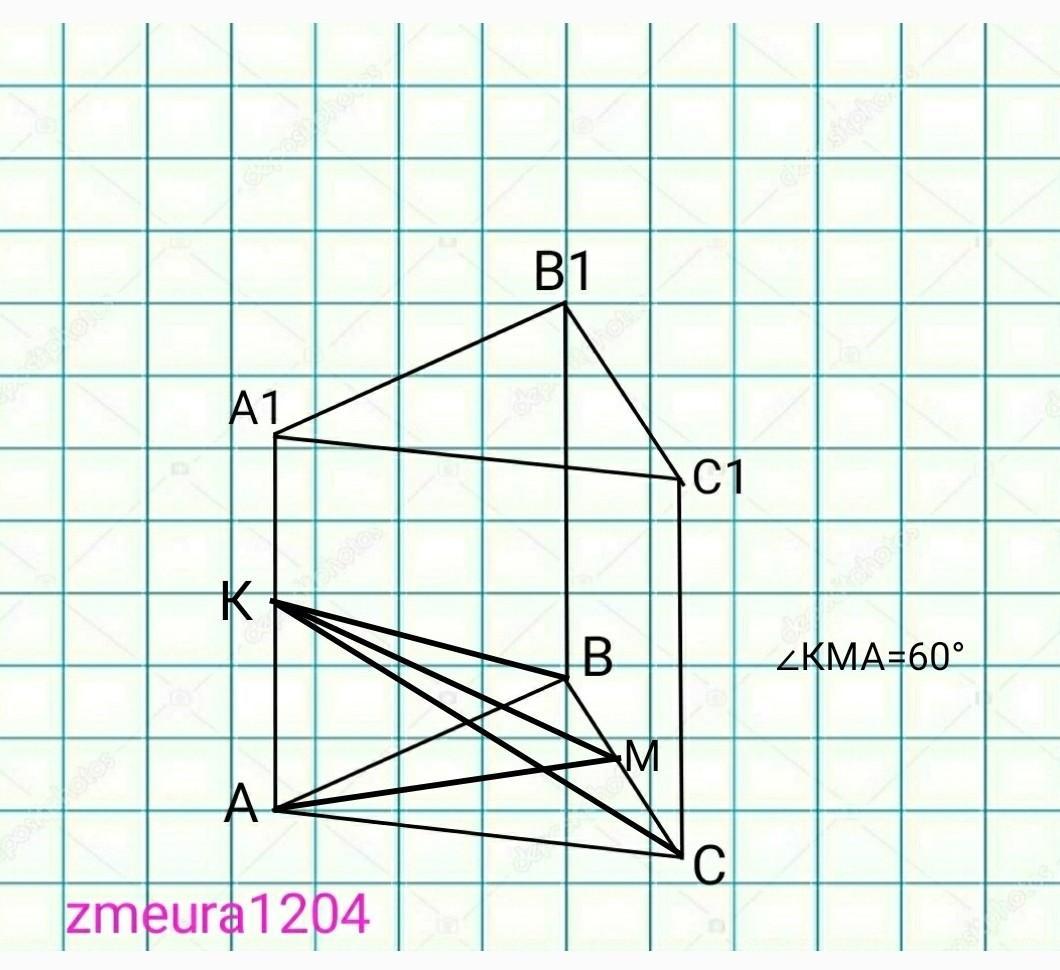
3) Сторона основания правильной треугольной призмы равна 6 см. Через сторону основания призмы проведено сечение, которое образует угол 60° с плоскостью основания и пересекает боковое ребро. Найдите площадь этого сечения.
Ответы на вопрос
Объяснение:
1)
сколько граней, ребер, вершин у призмы можно узнать с помощью формул(n - число сторон многогранника)
Количество граней равно n+2 ,где
n - боковые грани , 2 - основание призмы.
Количество ребер равно 3n.
Количество вершин равно 2n
14 -угольная призма:
Количество граней равно 14+2=16
Количество ребер равно 3•14=42
Количество вершин рано 2•14=28
2)
АВСDA1B1C1D1 - прямоугольный параллелепипед;
сторона а=9 см
сторона b=6 см
диагональ d=11 cм
Sпол поверх=?
Sполн. поверх=2•а•b+2•a•c+2•b•c
d²=a²+b²+c²
c=√(d²-a²-b²)=√(11²-9²-6²)=√4=2 см
Sполн поверх=2•9•6+2•9•2+2•6•2=
=108+36+24=168 см²
ответ: 168 см²
3)
АВСА1В1С1 - правильная треугольная призма
АВ=ВС=АС=6 см
ВСК - сечение
∠АНК=α=60°
найти : S(BCK)
решение:
АН проекция КН, КН⟂ВС, АН - медиана ,высота.
∆АВС - равносторонний:
АН=ВС•√3/2=6•√3/2=3√3 см.
∆КАН - прямоугольный:
cosa=AH/KH;
KH=AH/cosa=(3√3)/cos60=3√3/(1/2)=6√3 см
S(BCK)=1/2•BC•KH=1/2•6•6√3=18√3 см²
ответ: 18√3 см²


Объяснение:
1) 14- ребер в нижнем основании; 14-ребер в боковой поверхности; 14- ребер в верхнем основании. Всего: 14*3=32ребра.
...........
14- граней в боковой поверхности, 2- грани основания. Всего: 14+2=16 граней.
...........
14- вершин в верхнем основании, и 14- вершин в нижнем. Всего: 28 вершины.
________________
2)
АВ=СD=6см
ВС=АD=9см
А1С=11см
∆АВС- прямоугольный треугольник
По теореме Пифагора:
АС²=АВ²+ВС²=6²+9²=36+81=117см²
∆АА1С- прямоугольный треугольник
По теореме Пифагора:
АА1=√(А1С²-АС²)=√(11²-117)=
=√(121-117)=√4=2см
Р(ABCD)=2(AB+BC)=2(6+9)=
=2*15=30см
Sб=Р(ABCD)*AA1=30*2=60см²
S(ABCD)=AB*BC=6*9=54см²
Sпов=Sб+2*S(ABCD)=60+2*54=
=168см²
Ответ: Площадь поверхности параллелепипеда равна 168см²
____________
3)
АВ=ВС=АС=6см
∠КМА=60°
АМ- высота, медиана и биссектриса равностороннего треугольника ∆АВС.
АМ=АВ√3/2=6√3/2=3√3см.
∆КАМ- прямоугольный треугольник.
∠КАМ=90°; ∠КМА=60°;
∠АКМ=180°-∠КАМ-∠КМА=
=180°-90°-60°=30°
АМ- катет против угла 30°
КМ=2*АМ=2*3√3=6√3см
S(∆KBC)=½*KM*BC=½*6√3*6=18√3см²
Или решение 2)
S(∆ABC)=S(∆KBC)*cos∠KMA; →
S(∆KBC)=S(∆ABC)/cos60°;
S(∆ABC)=AB²√3/4=6²√3/4=9√3см²
S(∆KBC)=9√3/½=9√3/1*2/1=18√3см²
Ответ: площадь сечения равна 18√3см²