Question

ПОЖАЛУЙСТА МНЕ ОЧЕНЬ НУЖНО СРОЧНО ПЖ ПЖ ПЖ (Спасите меня пж
Я ВАС УЖЕ СПАСАЛ ВАЩА ОЧЕРЕДЬ ПОЖАЛУЙСТА
Задача внизу!!!!!!!!!!!!!!!!!!!!!!!

Две окружности вписаны в угол 60градусов, причем одна из них проходит через центр другой. Найдите отношение их радиусов.

Answer 1

Ответ:

Радиус меньшей окружности относится к радиусу большей как 1 к 2

Решение:

Смотрим чертежи!

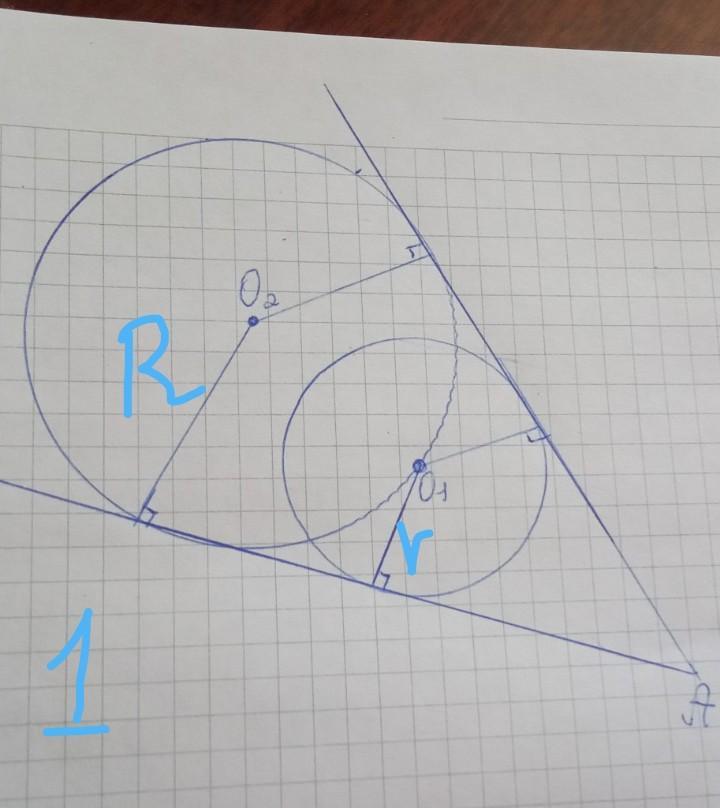
луч AO₁(O₂) - биссектриса ∠A

из ΔANO₂ (∠N = 90°) ∠O₂ = 90° - 30° = 60°

Получается прямоугольная трапеция у которой нижнее основание и боковая сторона равны R, а верхнее основание r.

cos 60° = (R - r) / R

0,5 = 1 - r/R

r/R = 0,5 или 1 ÷ 2

Answer 2

Ответ:

r/R=1/2

Объяснение:

• 1) строим угол А = 60° и 2 окружности (1 - с центром О1 и радиусом r, 2- с центром О2 и радиусом R), которые будут удовлетворять заданным условиям (рисунок 1)

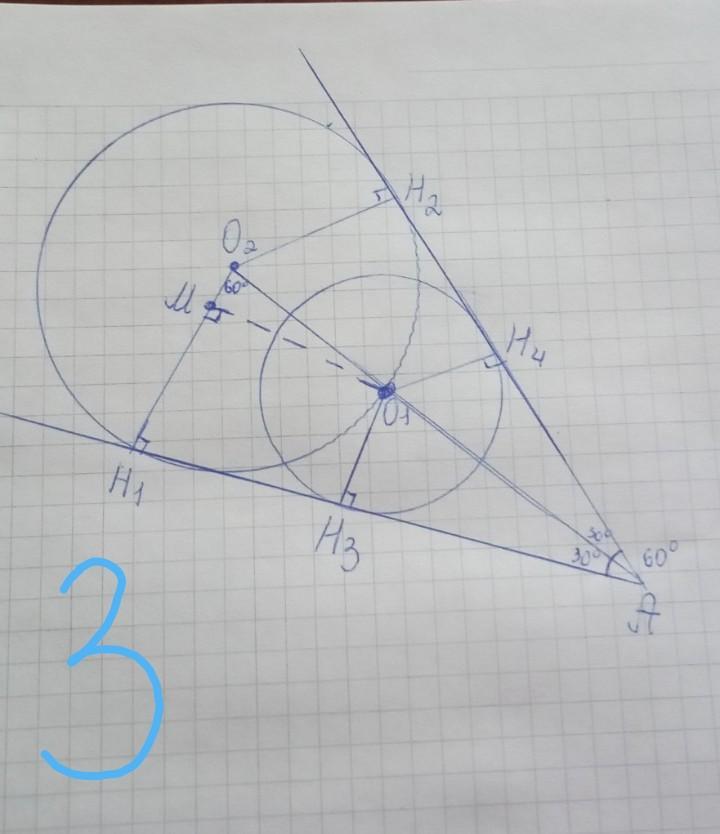
• 2) очевидно, что АН3=АН4, АН1=АН2 → АО2 - биссектриса угла А и О1 є АО2 (рисунок 2)

• 3) рассмотрим ∆АО2Н1: <Н1=90°, <А=30° → <О2=60°

проведём О1М || Н1Н3, где М є О2Н1. так как О2Н1 перпендикулярно Н1Н3, то и О2М перпендикулярно МО1 → <О2МО1=90° (рисунок 3)

• 4)Рассмотрим ∆О2МО1: <М=90°, <О2=60°(из пункта 3) → <О1=30°

Известно, что катет,лежащий напротив угла в 30° = половине гипотенузы, то есть О2М=О2О1/2.

то есть О2М=R/2. (рисунок 4)

• 5) Рассмотрим МО1Н3Н1: все углы = 90° и противоположные стороны параллельны → О1Н3=МН1

Но: О1Н3=r, а МН1=О2Н1-О2М=R-R/2=R/2 →

r=R/2 → r/R = (R/2)/R = 1/2 (рисунок 5)