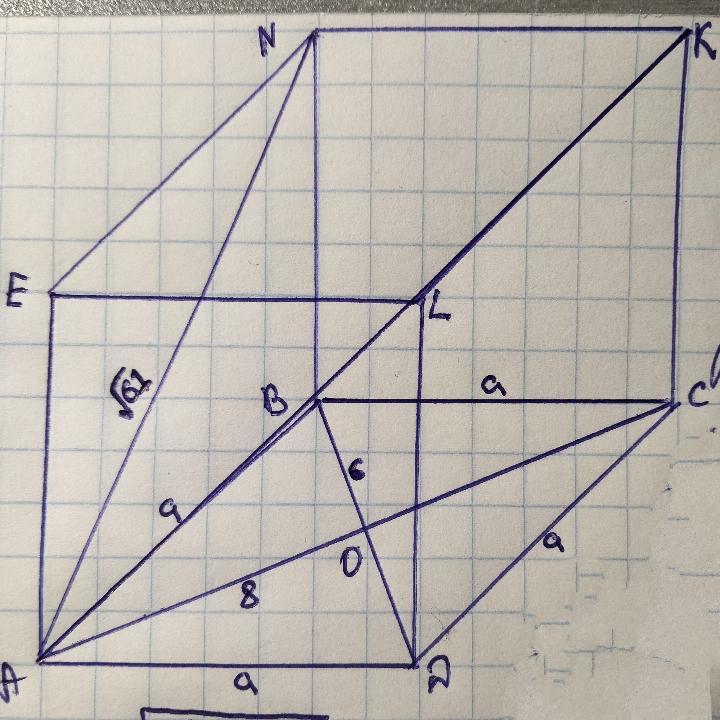
Письмово .Основою прямого паралелепіпеда є ромб з діагоналями 6 і 8см. Діагональ бічної грані дорівнює √61см. Знайти більшу діагональ паралелепіпеда і площу повної поверхні.
zmeura1204:
D=10; S=168
Ответы на вопрос
Ответил 1Manka1
2
Ответ:
10см; 168см²
Объяснение:
Ромбом называется параллелограмм, у которого все стороны равны.
АВ = ВС = СД = АД = а
АВСД - ромб
Формула стороны ромба через две диогонали:
а = (√(d1²+d2²)/2), где:
ВД = d1 = 6см;
АС = d2 = 8см
а = (√(6² + 8²)/2) = 5см
NB - высота параллелепипеда
Найдем высоту параллелепипеда по т. Пифагора:
NB = √(AN² - AB²), где:
АN = √61см
NB = √(√61² - 5²) = √36 = 6см
NB = KC = 6см
Найдем наибольшую диагональ параллелепипеда за т. Пифагора:
АК = √(КС² + АС²) = √(6² + 8²) =
= √100 = 10см
Площадь полной поверхности:
Sп = Sб + 2Sо, где:
Sп - полная поверхность;
Sб - боковой поверхности;
Sо - основы;
Sб = Ро * высоту = 4 * 5 * 6 =
= 120см²
So = 1/2 * d1 * d2 = 1/2 * 6 * 8 = 24
Sп = 120 + 2 * 24 = 168см²
Приложения:
Новые вопросы