Question

основание трапеции равны 10 и 11 найдите больший из отрезков на которые делит среднюю линию этой трапеции одна из и ее диагоналей. Решение через подобие треугольников. ПОЖАЛУЙСТА как МОЖНО Скорее!!!​

Answer 1

Ответ:

Пошаговое объяснение:

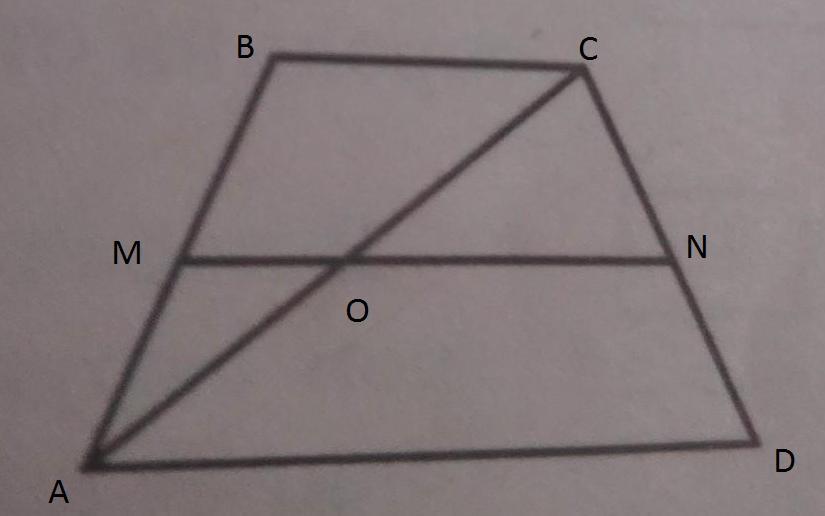
Рассмотрим трапецию ABCD, в которой BC и AD - основания и соответственно равны 10 и 11, MK - средняя линия, O - пересечение АС и MK.  

Рассмотрим два треугольника ABC и ACD. В Δ ABC MO - средняя линия треугольника, MO = 1/2 * BC = 10/2 = 5. В Δ ACD OK - средняя линия треугольника, OK = 1/2 * AD = 11/2 = 5.5.  

Ответ: большим из отрезков, на которые делит среднюю линию трапеции одна из ее диагоналей является отрезок OK = 5.5.

Answer 2

Ответ: 5,5

Пошаговое объяснение:

MN║BC║AD

ABC подобен AMO, причем МО:ВС=1:2, поскольку их высоты находятся в таком соотношении (MN-средняя линия трапеции)

ACD подобен  OCN, причем ON:AD=1:2⇒ ON=11:2=5,5

Answer 3

надо же... даже в буквах совпали решения))