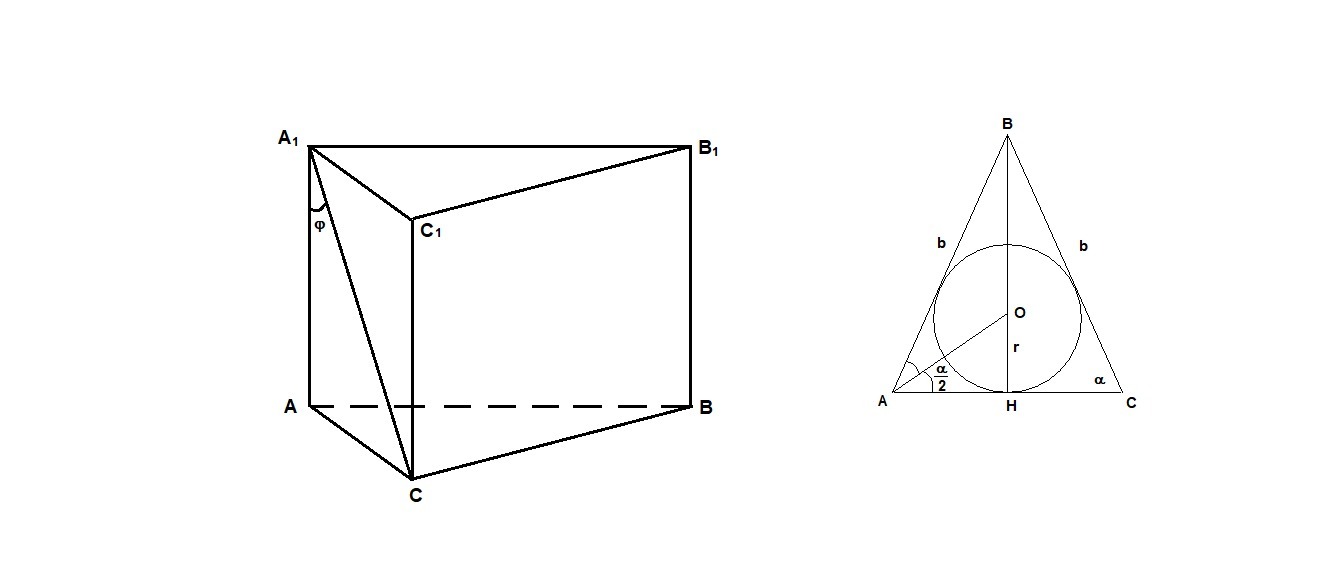
Основание прямой призмы равнобедренный треугольник с боковой стороной b и углом при основании a. Диагональ боковой грани, содержащей основание треугольника, образует с боковым ребром угол f. Найдите объём цилиндра, вписанного в призму
Ответы на вопрос
Дано: АВСА₁В₁С₁ - прямая призма,
ΔАВС: АВ = ВС = b, ∠ВАС = α,
∠АА₁С = φ.
Цилиндр вписан в призму.
Найти: Объем цилиндра.
Решение:
Если цилиндр вписан в призму, то основания цилиндра вписаны в основания призмы, а высоты равны.
Радиус основания цилиндра - радиус окружности, вписанной в треугольник АВС.
Пусть ВН - высота ΔАВС. А так как он равнобедренный, то и медиана.
ΔВСН: СН = ВС · cosα = b · cosα.
AH = CH = b·cosα
AC = 2b·cosα
Центр вписанной окружности - точка О - точка пересечения биссектрис.
АО - биссектриса угла А, ОН - радиус вписанной окружности, ∠ОАН = α/2.
ΔАОН: ОН = АН · tg(α/2)
r = b·cosα · tg(α/2)
ΔAA₁C: AA₁ = AC · ctg φ - высота призмы и цилиндра,
h = 2b·cosα · ctgφ
Vцил = πr²h
Vцил = π · (b·cosα · tg(α/2))² · 2b·cosα · ctgφ
Vцил = 2b³π·cos³α · tg²(α/2) · ctgφ