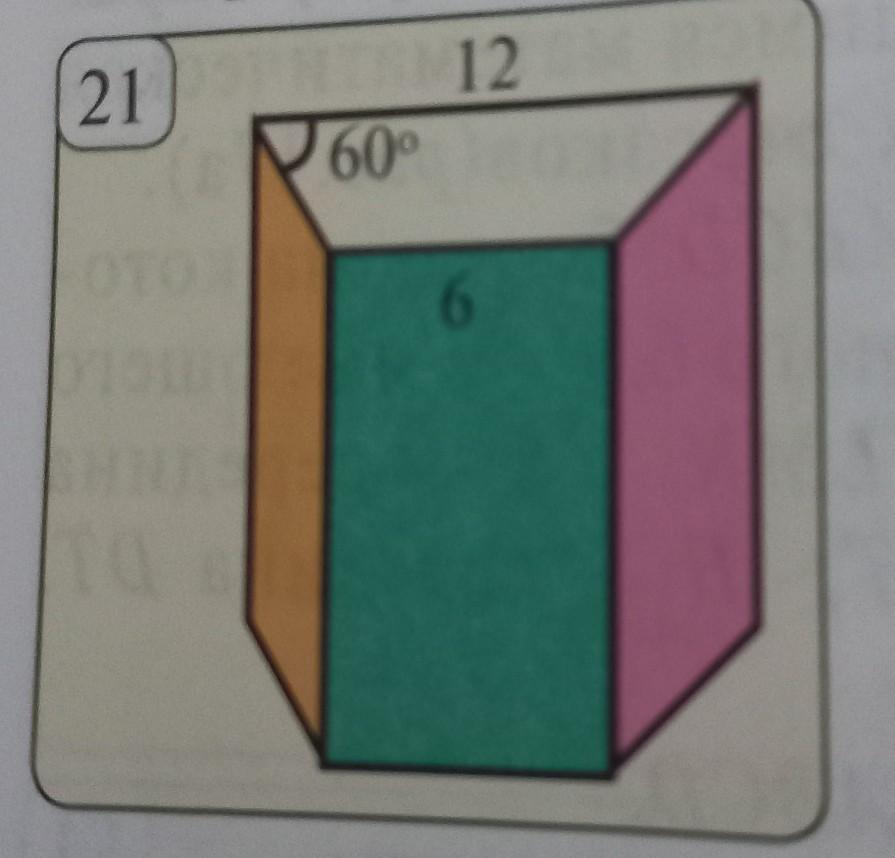
основание прямой призмы изображённой на рисунке 21 равнобедренная трапеция Основания трапеции 12 см и 6 см один из углов при основании равен 60° Пусть большая грань призмы квадрат Найдите площадь полной поверхности призмы
Приложения:
Ответы на вопрос
Ответил natalyabryukhova
21
Ответ:
(360+54√3)см²
Объяснение:
Дано: прямая призма;
АЕКВ - равнобедренная трапеция;
∠АЕК=60°; АВ=6 см; ЕК=12 см;
FEKH - квадрат.
Найти: Sполн.
Решение:
FEKH - квадрат ⇒FE=EK=12 см
Sполн.=Sбок.+2Sосн.
Найдем площадь основания.
Для нахождения АР, рассмотрим ΔЕРА - прямоугольный.
∠Е=60° ⇒ ∠ЕАР=90°-60°=30° (сумма острых углов прямоугольного треугольника)
(свойство равнобедренной трапеции)
ЕР=(12-6):2=3 (см)
⇒ АЕ=ЕР·2=6(см) (катет, лежащий против угла 30°)
По теореме Пифагора:
АР²=АЕ²-ЕР²=36-9=27
АР=3√3 (см)
(см²)
Найдем Sбок.:
Sбок.=Росн.·ЕF
Sбок.=(12+6+6+6)·12=360 (см²)
⇒ Sполн.=360+2·27√3=(360+54√3)(см²)
Приложения:

Новые вопросы
Русский язык,
2 года назад
Математика,
2 года назад
Экономика,
7 лет назад
Алгебра,
7 лет назад
Математика,
8 лет назад