Очень срочно нужна помощь
Приложения:

Ответы на вопрос
Ответил Аноним
1
Ответ:
4
Объяснение:
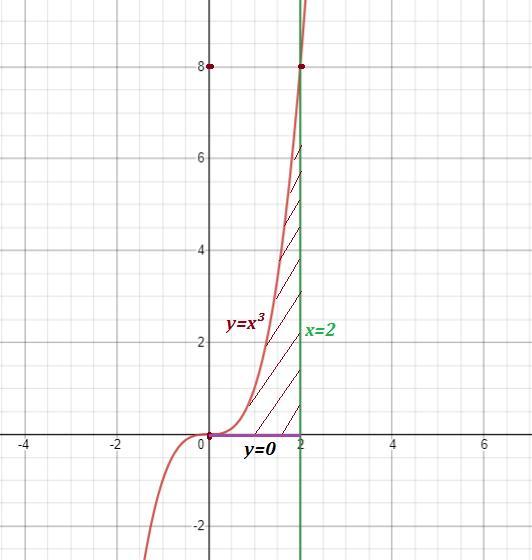
х³=0; х=0, х=2- пределы интегрирования . первообразная функции х⁴/4, воспользуемся формулой Ньютона - Лейбница, получим площадь 2⁴/4-0⁴/4=16/4=4
Ответил NNNLLL54
0
Ответ:
Ищем площадь с помощью определённого интеграла.
Приложения:
Новые вопросы
Русский язык,
1 год назад
Алгебра,
6 лет назад