Найти значение выражения
Ответ должен выйти 1, но как к ней придти- не знаю. Буду рада помощи ))
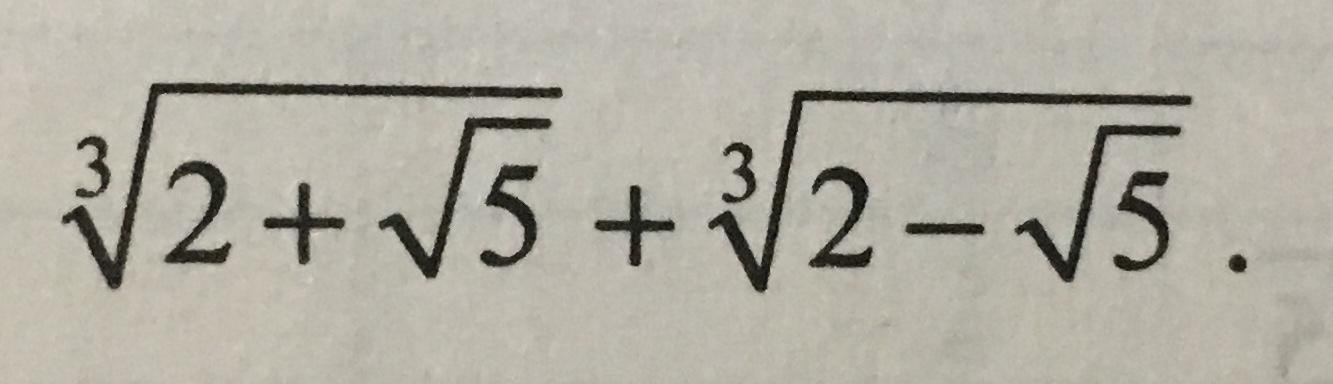
в комментариях трудно написать {{{{{
Ответы на вопрос
Ответ:1
Объяснение:∛(2+√5) +∛(2-√5)=х возведем в куб обе части равенства
2+√5+3·(∛2+√5)²·∛(2-√5)+3∛(2+√5)·(∛2-√5)²+2-√5=х³;
4+3∛(2+√5)·∛(2-√5)(∛(2+√5) +∛(2-√5))=х³;
4+3∛(2²-(√5)²)· х=х³;
4-3х=х³⇒ х³+3х-4=0⇒х=1---находим подбором с проверкой.
х³+3х-4=(х-1)(х²+х+4), x²+x+4=0--корней не имеет
подбор корней связан с корнями из пяти - трудно чтото подобрать но можно
подобрал !!!!!!
(2+√5) = 1/8 + 3√5/8 + 15/8 + 5√5/8 = (1/2 + √5/2)³ = (1 + √5)³/8
(2 - √5) = 1/8 - 3√5/8 +15/8 - 5√5/5 = (1/2 - √5/2)³ = (1 - √5)³/ 8
∛(2 + √5) + ∛(2 - √5) = ∛(1 + √5)³/2³ + ∛(1 - √5)³/2³ = (1 + √5)/2 + (1 - √5)/2 = 1/2 - √5/2 + 1/2 + √5/2 = 1
Ответ ОДИН
сделаем по другому
a = 2 + √5
b = 2 - √5
∛(2 + √5) + ∛(2 -√5) = c
∛(a*b) = ∛((2 + √5)(2 - √5)) = ∛(-1) = -1 (формула 1)
a + b = 2 + √5 + 2 - √5 = 4 (формула 2)
∛a + ∛b = c
∛a = c - ∛b (возводим в куб) (формула 3)
a = c³ - 3c²∛b + 3c∛b² - b
c³ = a + 3c²∛b - 3c∛b² + b = a + b + 3c∛b(c - ∛b) ={ по формуле 2 и 3} = 4 + 3c∛b*∛a = {формула 1} =4 - 3c
c³ + 3c - 4 = 0
c³ + c² + 4c - c² - c - 4 = 0
c²(c - 1) + c(c -1) + 4(c-1) = 0
(c - 1)(c² + c + 4) = 0
вспоминаем что ∛(2 + √5) + ∛(2 -√5) = c
первая скобка c = 1
вторая скобка c² + c + 4 = 0 D=1 - 4*4 = -15 дискриминант отрицательный, действительных решений нет (2 комплексных)
Ответ 1
разложение много времени заняло, чтото не получалось
или попробовать использовать формулу сложного радикала