Найдите наименьшее целое значение параметра a, при котором функция y=(a^2+a-30)x+a убывает на множестве действительных чисел.
Ответы на вопрос
Ответил Medved23
1
Ответ: а = -5.
Объяснение: Функция - линейная. Она убывает, если коэффициент перед х меньше 0.
a² + a - 30 < 0
(a - 5)(a + 6) < 0 ⇒ а ∈ (-6; 5).
Наименьшее целое значение параметра, удовлетворяющее неравенству - а = -5.
Приложения:
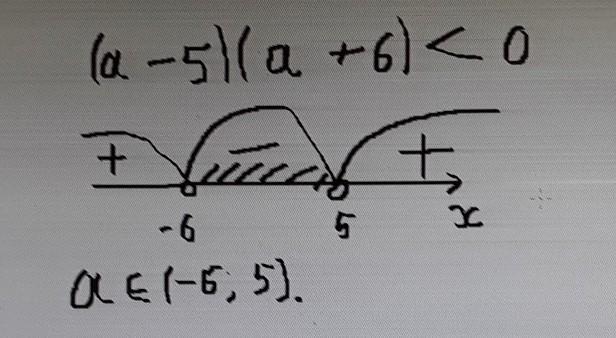
Sews123s:
Ответ 5 ? Или -5?
-5
Можешь обьяснить почему ? Ведь минус на минус даёт плюс в последнем действии
вконце не минус а, просто а. это тире, а не минус
Тогда откуда в принципе -5? Если корень из уравнения -6;5
если а = -6 или а = 5, то функция вообще не будет линейной и не будет ни убывать, ни возрастать. Чтобы она чисто убывала, она должна быть в пределах от -6 до 5, т.е. любое значение между этими числами. Самое маленькое значениа а, которое под это условию подходит - это а = -5
Все понял, спасибо большое!
Новые вопросы
Математика,
1 год назад
Английский язык,
1 год назад
Алгебра,
1 год назад
Английский язык,
1 год назад
Химия,
7 лет назад
Қазақ тiлi,
7 лет назад