Найдите наибольшее целое значение x из области определения функции
Приложения:
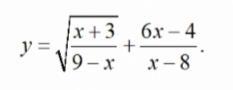
mic61:
+7
Ответы на вопрос
Ответил Alnadya
3
Решение.
Подкоренное выражение должно быть неотрицательным, знаменатель дроби не должен быть равен нулю .
Решаем неравенство методом интервалов.
Знаки функции:
3) Находим пересечение двух множеств.
Ответ: наибольшее целое - это х=7 .
Новые вопросы
Українська література,
2 года назад
Литература,
2 года назад
Русский язык,
2 года назад
Математика,
8 лет назад