На уроке решали задачу по геометрии. Два внешних угла треугольника при разных вершинах равны. Периметр треугольника равен 74 см, а одна из сторон равна 16 см. Найдите две другие стороны треугольника. В классе сначала доказывали, что треугольник равнобедренный, а потом находили 2 стороны. Но как у треугольника, у которого разные вершины, 2 угла могут быть одинаковыми?
Приложения:

Ответы на вопрос
Ответил Hrisula
0
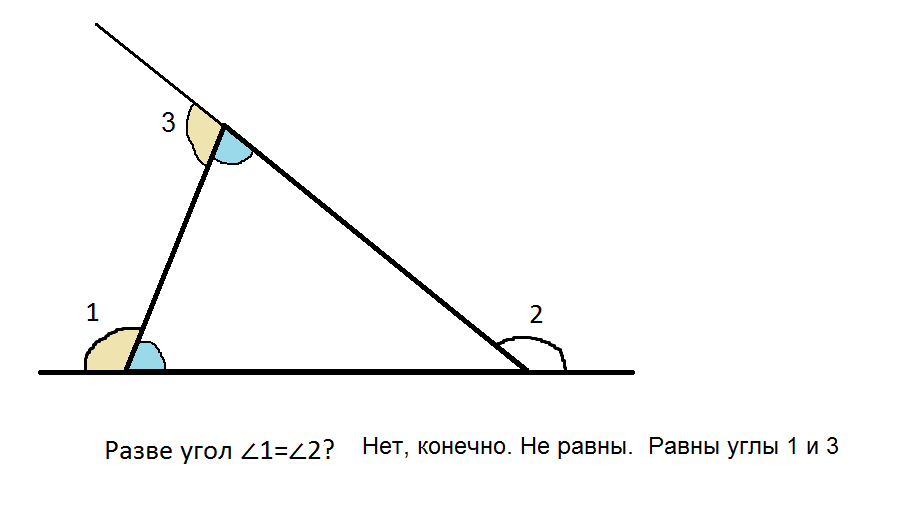
Внешние углы и смежные с ними внутренние в сумме дают величину развернутого угла, т.е. 180.
Значи, внутрении углы при той же стороне тоже равны между собой.
Треугольник с равными углами при одной из сторон - равнобедренный ( свойство).
Тогда основание этого треугольника 16 см, сумма двух других
74-16=58 см,
и каждая боковая сторона равна
58:2=29 см
Боковая сторона не может быть равной 16 см, т.к. основание получится больше суммы боковых сторон, такой треугольник существовать не может.
74-16*2=42. Не подходит.
Значи, внутрении углы при той же стороне тоже равны между собой.
Треугольник с равными углами при одной из сторон - равнобедренный ( свойство).
Тогда основание этого треугольника 16 см, сумма двух других
74-16=58 см,
и каждая боковая сторона равна
58:2=29 см
Боковая сторона не может быть равной 16 см, т.к. основание получится больше суммы боковых сторон, такой треугольник существовать не может.
74-16*2=42. Не подходит.
Приложения:
Ответил Hrisula
0
Внешний+внутренний углы=180º Отсюда и исходите.
Ответил K04LA
0
Так что значит разные вершины? Разные вершины - это ведь разные углы треугольника.
Ответил Hrisula
0
Верно. Но углы в треугольники могут быть как разными ВСЕ, могут быть равны два угла, ( внешние при них равны), могут быть равны ВСЕ углы, и внешние при всех трех вершинах ( а это ведь не одна и та же вершина) будут равны.
Ответил K04LA
0
Вот. Спасибо вам за ответ.
Ответил Hrisula
0
Вы разобрались. Это главное.
Новые вопросы
Русский язык,
2 года назад
Биология,
2 года назад
Математика,
9 лет назад
Физика,
9 лет назад
Алгебра,
9 лет назад