На сторонах ВС і B_{1}*C_{1} трикутників ABC і A,B,C, позначили відповідно точки Di*D_{1} Доведіть рівність трикутни ків ABCi*A_{1}*B_{1}*C_{1} , якщо AB = A_{1}*B_{1} BD = B_{1}*D_{1} , AD = A_{1}*D_{1} CD = C_{1}*D_{1} >
Приложения:

Ответы на вопрос
Ответил MysticalOrient
3
Ответ:
Дано: трик. АВС і А1В1С1; точки D i D1; АВ=В1D1; ВD=В1D1; АD=A1D1; СD=C1D1
Довести: АВС= А1В1С1
Розглянемо трикутники ABD та A1B1D1.
За умовою задачі BD = B1D1, AD = A1D1, тому сторони AB та D,D1 паралельні (за теоремою про серединну лінію у трикутнику), а отже, по теоремі про паралельні сторони, маємо:
ABD =A1B1D1.
Аналогічно, розглядаючи трикутники B1C1D1 та BCD, можемо зробити висновок:
B1C1D1 = BCD.
За теоремою про трикутники, трикутники ABC і трикутник A1B1C1 рівні, якщо їх сторони відповідно рівні. А ми вже довели рівність сторін трикутників ABC і A1B1C1. Тому, за теоремою про трикутники, маємо:
ABC = A1B1C1.
(Рисунок зліва, розв'язання справа)
Приложения:
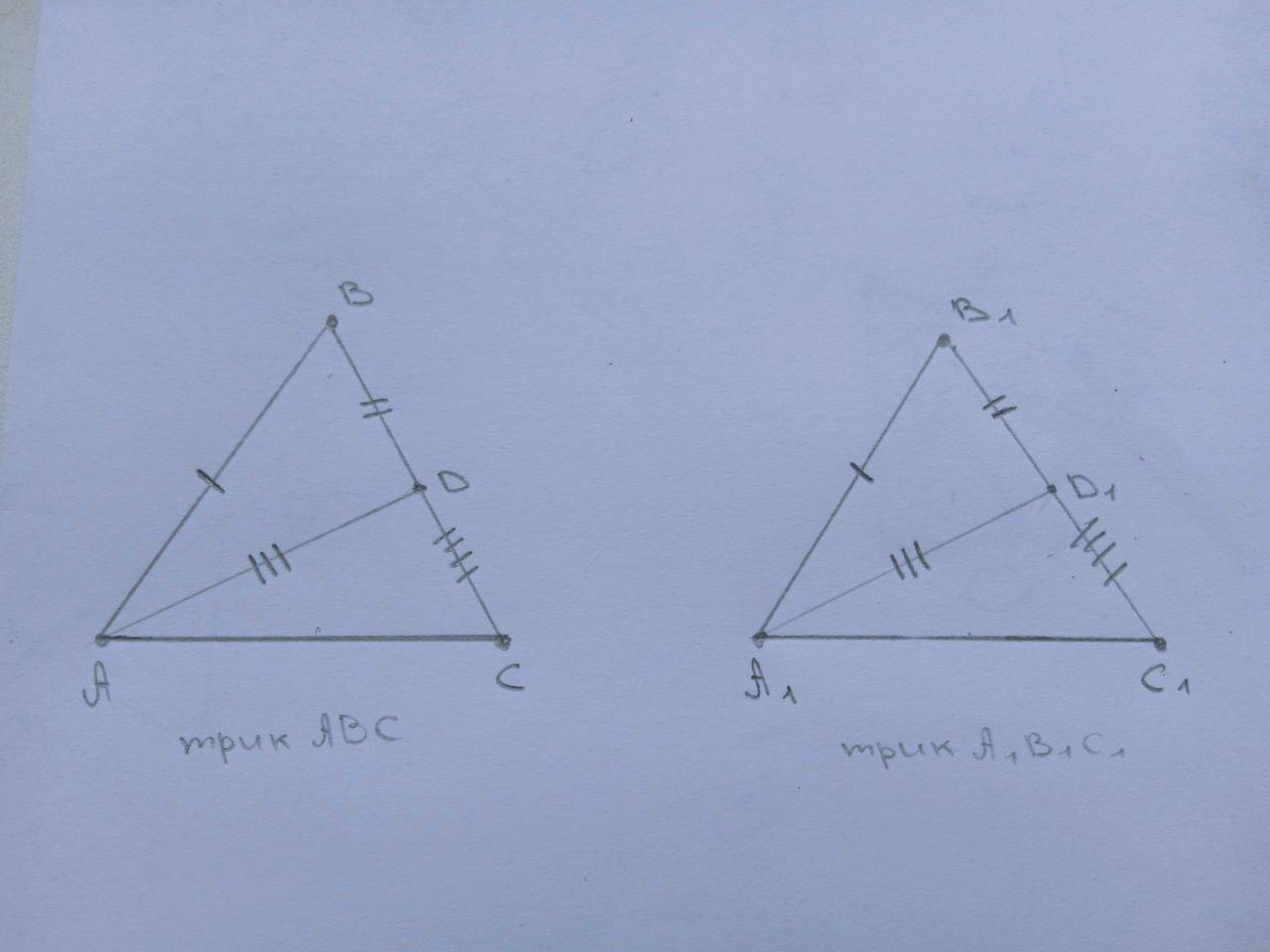
Новые вопросы
Українська мова,
1 год назад
Українська мова,
1 год назад
Литература,
1 год назад
Математика,
6 лет назад
Английский язык,
6 лет назад