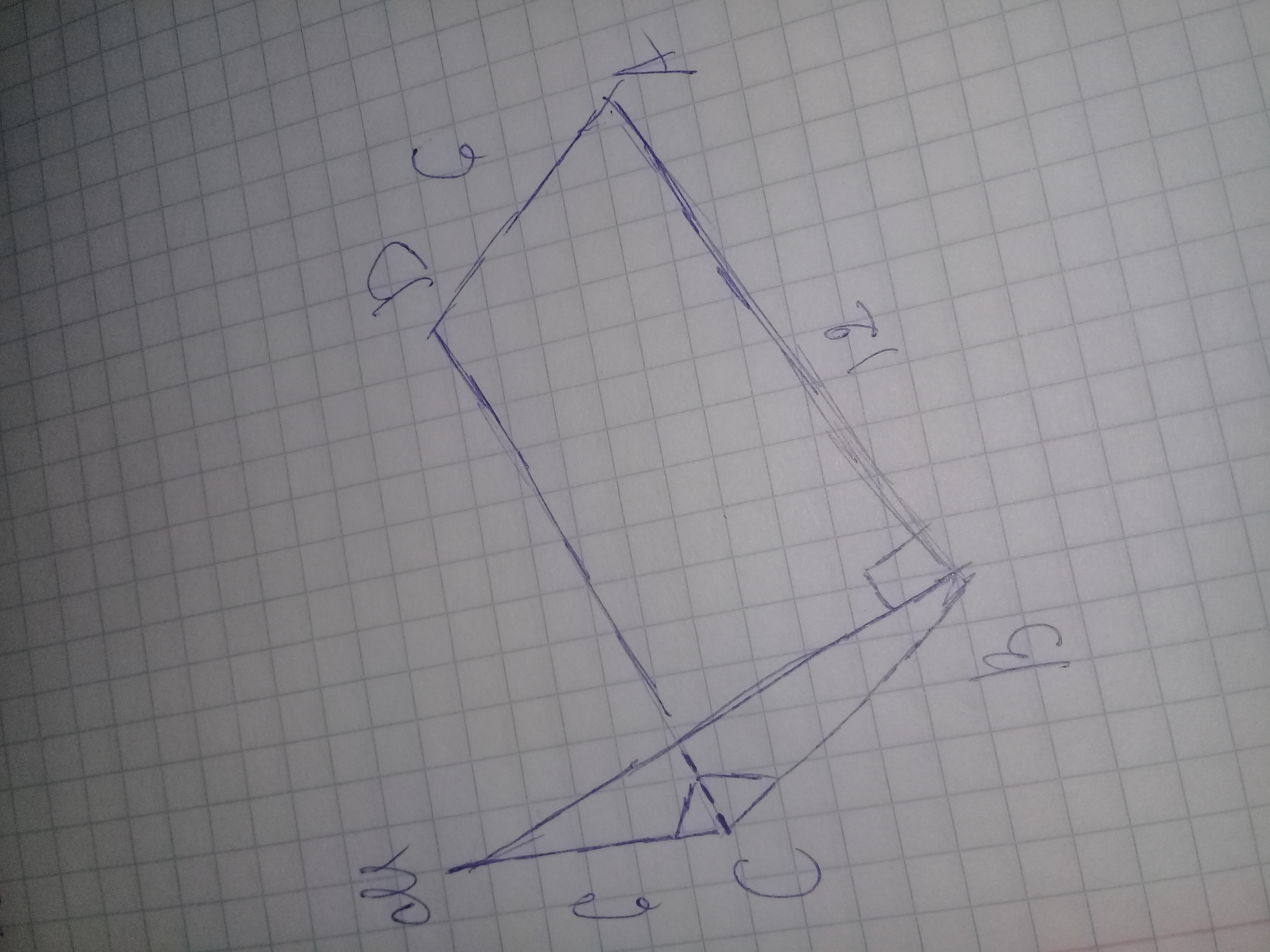
из вершины C прямоугольника ABCD со сторонами 6 см и 12 см к его плоскости проведён перпендикуляр CM равен 6 см. Найти расстояние от точки м до прямых BP и BA
Помогите нарисовать рисунок составить дано и решение
Ответы на вопрос
Ответил polfunk2016
0
Кратчайшим расстоянием от точки до прямой является длина перпендикуляра, опущенного из этой точки на эту прямую.
Расстоянием от точки М до прямой BC является длина перпендикуляра CM = 6 cм.
Если прямая (AB), проведенная на плоскости через основание (B) наклонной (МВ), перпендикулярна её проекции (CB), то она перпендикулярна и самой наклонной (теорема о трех перпендикулярах)
⇒ Расстоянием от точки М до прямой AB отрезок MB
Если BC = 6 cм, AB = 12 см
По теореме Пифагора:
MB² = BC² + CM²
MB² = 6² + 6² = 72
MB = √72 = 6√2 (см)
Расстоянием от точки М до прямой BC является длина перпендикуляра CM = 6 cм.
Если прямая (AB), проведенная на плоскости через основание (B) наклонной (МВ), перпендикулярна её проекции (CB), то она перпендикулярна и самой наклонной (теорема о трех перпендикулярах)
⇒ Расстоянием от точки М до прямой AB отрезок MB
Если BC = 6 cм, AB = 12 см
По теореме Пифагора:
MB² = BC² + CM²
MB² = 6² + 6² = 72
MB = √72 = 6√2 (см)
Приложения:
Новые вопросы
Русский язык,
2 года назад
Другие предметы,
2 года назад
Геометрия,
8 лет назад
Литература,
9 лет назад
Химия,
9 лет назад