исследовать ряды на сходимость
Приложения:
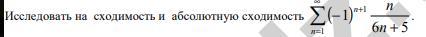

Ответы на вопрос
Ответил MrSolution
1
Ответ:
(см. объяснение)
Пошаговое объяснение:
Проверим, будет ли n-ый член ряда стремиться к нулю:
Получили, что не выполнен необходимый признак сходимости ряда, а значит ряд расходится.
Поскольку ряд расходится, то исходный ряд
также расходится.
Задание выполнено!
Новые вопросы
Русский язык,
9 месяцев назад
Оʻzbek tili,
9 месяцев назад
Українська література,
1 год назад
Українська мова,
1 год назад