Хотябы первые 2 задания молю
Приложения:
Ответы на вопрос
Ответил NNNLLL54
0
Ответ:
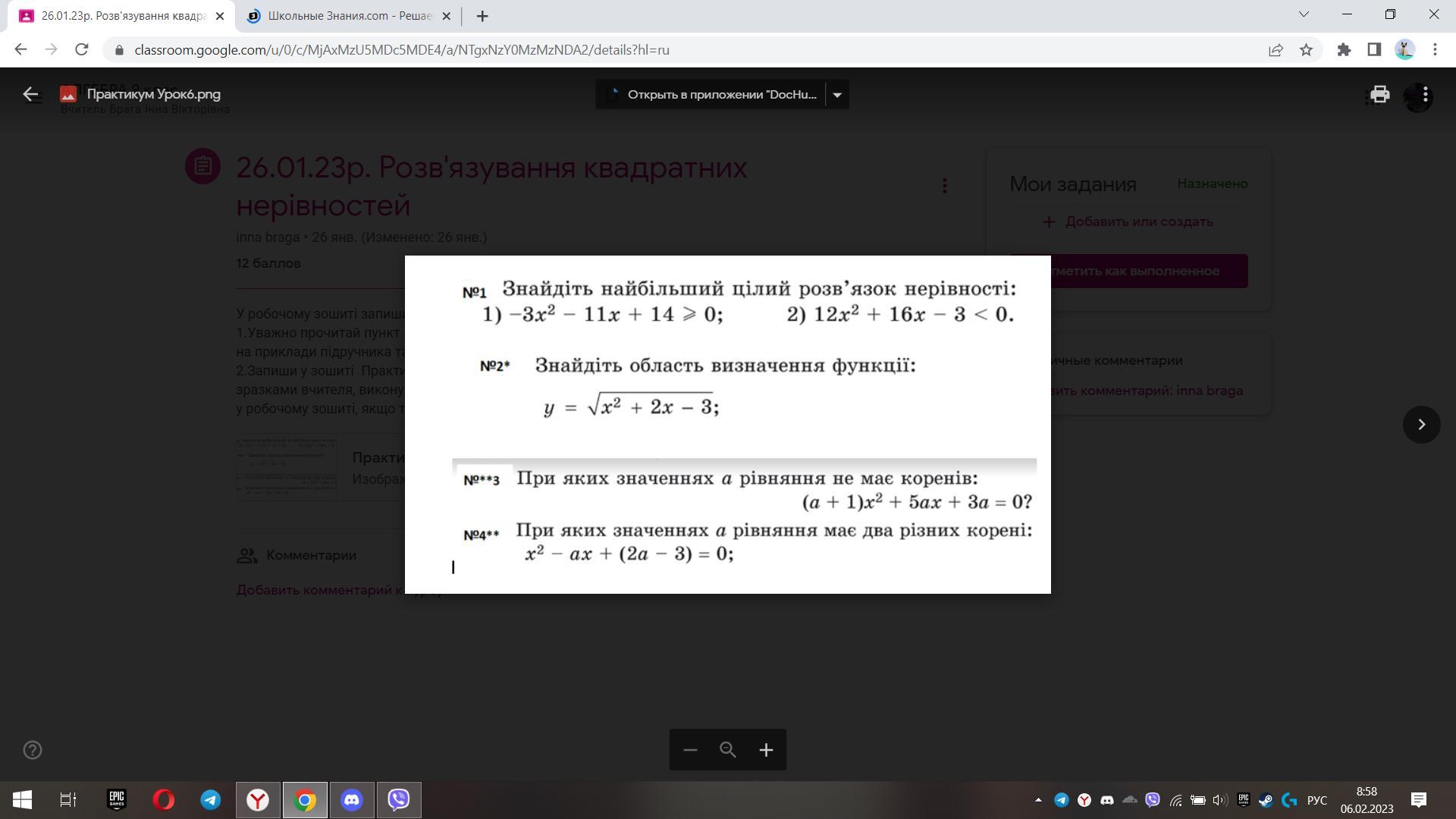
1) Решить неравенство .
Перепишем неравенство в виде . Решаем его методом интервалов .
Знаки функции:
Наибольшее целое решение неравенства : .
Наибольшее целое решение - .
2) Найти область определения функции .
Подкоренное выражение должно быть неотрицательным .
dasaforostana96:
здравствуйте, помогите пожалуйста с алгеброй, последние задание в моем профиле
Новые вопросы
Другие предметы,
9 месяцев назад
Українська мова,
9 месяцев назад
История,
1 год назад
Окружающий мир,
1 год назад
Алгебра,
6 лет назад
Математика,
6 лет назад