ГЕОМЕТРИЯ РЕШИТЬ СРОЧНО
Приложения:
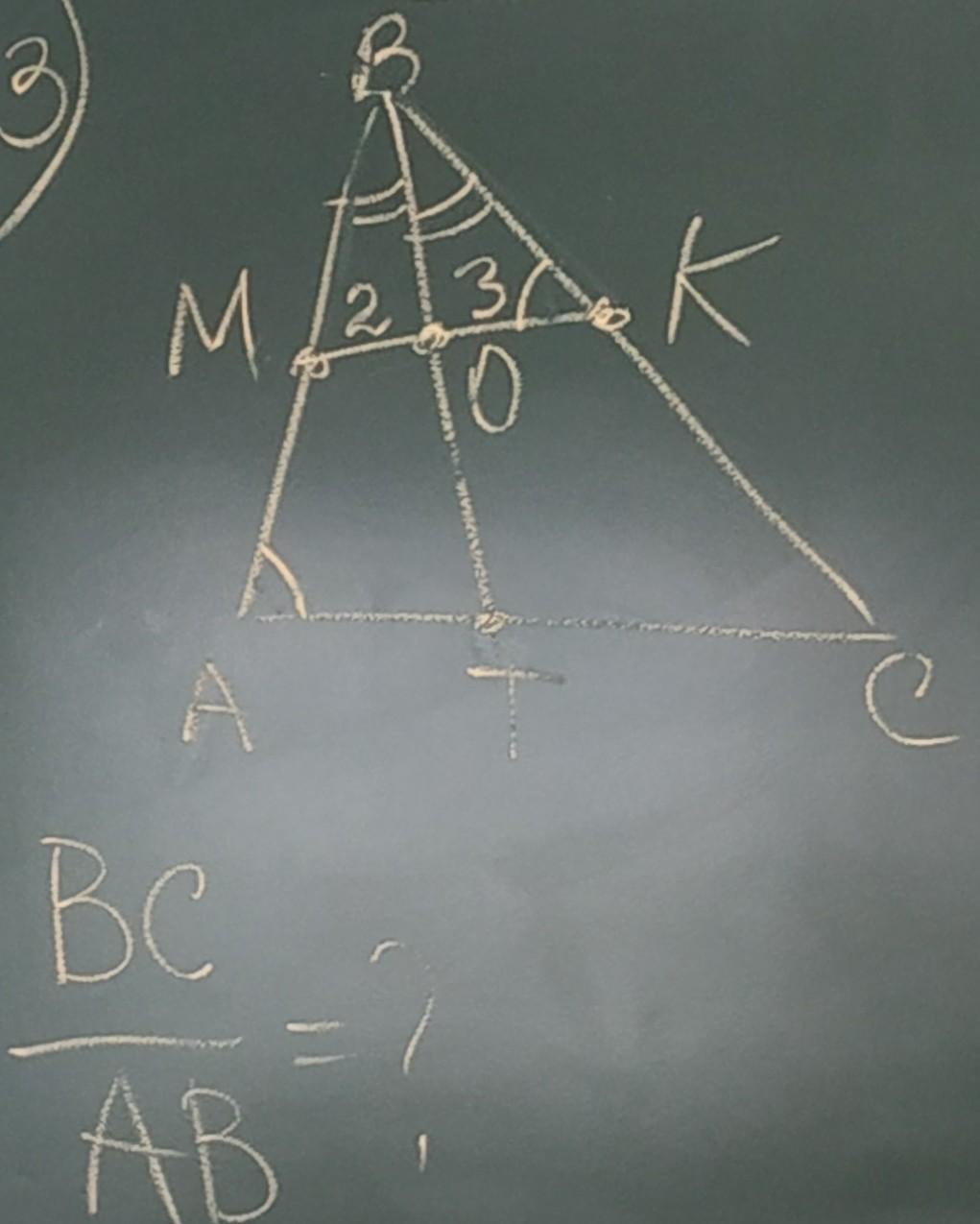
Ответы на вопрос
Ответил Hrisula
3
Прямая пересекает стороны треугольника АВС в точках М и К, М ∈ АВ, К ∈ ВС. угол ВКМ=угол ВАС; ВО - биссектриса треугольника МК, при этом МО:ОК=2:3. Найти ВС:АВ.
Ответ: ВС:АВ =2:3
Объяснение:
По свойству биссектрисы ВО делит сторону МК в отношении ВМ:ВК=МО:ОК=2:3
Рассмотрим ∆ АВС и ∆ МВК. Угол В - общий, угол ВКМ=ВАС.
Два треугольника подобны, если два угла одного треугольника соответственно равны двум углам другого.
Из подобия следует отношение ВС:АВ=ВМ:ВК.⇒
ВС:АВ=2:3.
Приложения:

kpdalka:
спасибо большое
Новые вопросы
Русский язык,
2 года назад
Русский язык,
2 года назад
Алгебра,
2 года назад
Английский язык,
2 года назад
Литература,
8 лет назад
Алгебра,
8 лет назад