геометрия
17;18;20__
Ответы на вопрос
Ответ:
Объяснение:
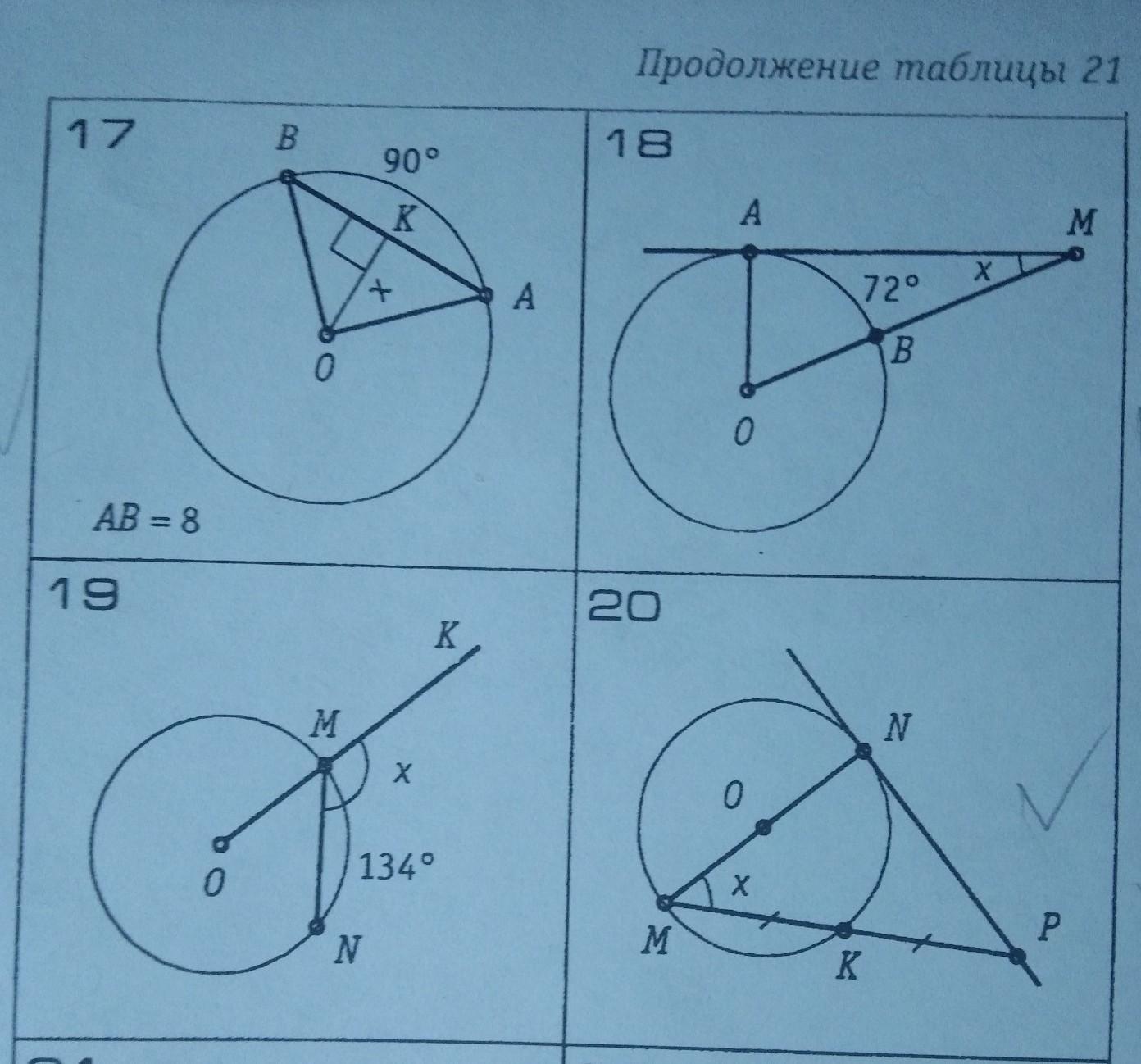
17. Центральный <AOB опирается на дугу 90°, значит <AOB=90°.
АО=ОВ - радиусы => прямоугольный тр-к △АОВ также р/б. Значит его высота ОК также медиана и биссектриса и <OBK=<BOK=45°. А значит △BKO прямоугольный и р/б и OK=BK=AB/2=8/2=4
x=4
18. Центральный <AOB опирается на дугу 72°, значит <AOB=72°.
Радиус окружности, проведенный в точку касания, перпендикулярен касательной.
Значит тр-к △АОМ - прямоугольный, <OAM=90°, <AOM=72°, x=90-72=18°.
20. ON⊥NP, △MNP - прямоугольный.
Вписанный угол <MKN опирается на диаметр, значит <MKN=90°.
MK=KP по условию рисунка, значит NK - высота и медиана.
Если медиана треугольника является его высотой, то этот треугольник — равнобедренный.
=> △MNP - прямоугольный и р/б и тогда х=45°