Два правильных треугольника АBC и DBС расположены так, что их плоскости взаимно перпендикулярны.Найти тангенс двугранного угла образованного плоскостями ADC и ABC
Ответы на вопрос
Ответил nafanya2014
1
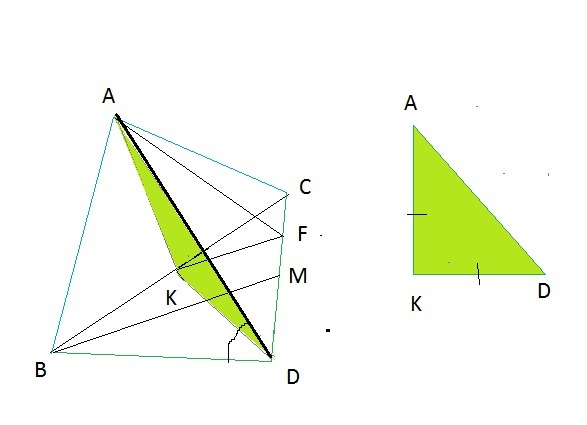
АК- высота, медиана и биссектриса треугольника АВС
DК- высота, медиана и биссектриса треугольника DВС
∠AKD- линейный угол двугранного угла между пл. АВС и пл. DВС
∠AKD=90°
ВМ- высота, медиана и биссектриса треугольника АВС
КF|| BM
KF=BM/2
KF⊥CD
AF⊥CD по теореме о трех перпендикулярах
∠AFK- линейный угол двугранного угла между пл.ADC и пл. ABC
Пусть АВ=ВС=АС=ВD=CD=a
АК=DK=BM=а√3/2
KF=a√3/4
Из прямоугольного треугольника АКF
tg∠AFK=AK/KF=2
DК- высота, медиана и биссектриса треугольника DВС
∠AKD- линейный угол двугранного угла между пл. АВС и пл. DВС
∠AKD=90°
ВМ- высота, медиана и биссектриса треугольника АВС
КF|| BM
KF=BM/2
KF⊥CD
AF⊥CD по теореме о трех перпендикулярах
∠AFK- линейный угол двугранного угла между пл.ADC и пл. ABC
Пусть АВ=ВС=АС=ВD=CD=a
АК=DK=BM=а√3/2
KF=a√3/4
Из прямоугольного треугольника АКF
tg∠AFK=AK/KF=2
Приложения:
Ответил Аноним
0
спасибо большое!
Новые вопросы
Қазақ тiлi,
2 года назад
Алгебра,
9 лет назад