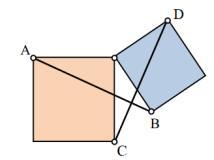
Два квадрата на рисунке имеют общую вершину.
a) Докажите, что отрезки АВ и CD равны.
б) Верно ли, что эти отрезки перпендикулярны?
Приложения:
Ответы на вопрос
Ответил natalyabryukhova
2
Ответ:
Доказано: а) АВ = CD; б) AB ⊥ CD
Объяснение:
Два квадрата на рисунке имеют общую вершину.
a) Докажите, что отрезки АВ и CD равны.
б) Верно ли, что эти отрезки перпендикулярны?
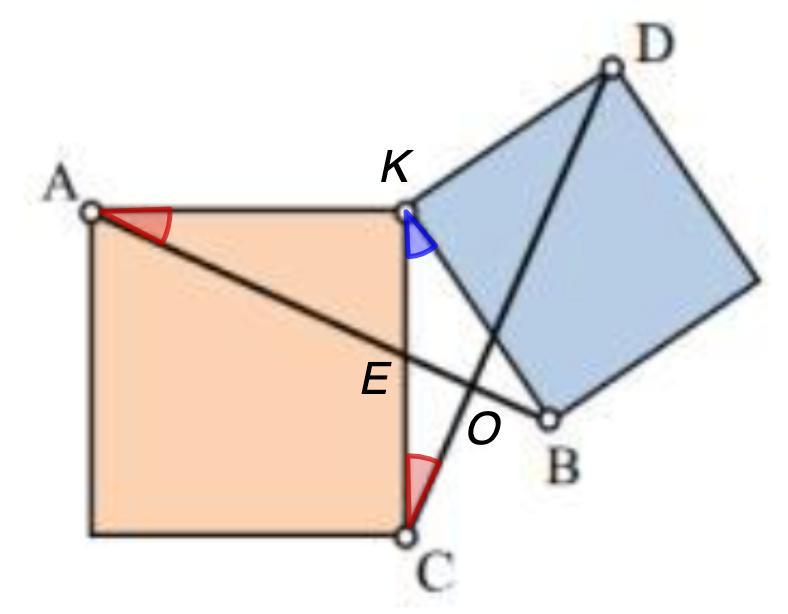
Дано: Два квадрата имеют общую вершину К;
Доказать: АВ = СD; AB ⊥ CD
Решение:
а) Рассмотрим ΔАКВ и ΔСКD.
АК = КС; КВ = КD.
∠AKB = 90° + ∠CKB
∠CKD = 90° + ∠CKB
⇒ ∠AKB = ∠CKD
ΔАКВ = ΔСКD (по двум сторонам и углу между ними, 1 признак)
- В равных треугольниках против равных углов лежат равные стороны.
⇒ АВ = CD
б) Рассмотрим ΔАКЕ и ΔСОЕ.
∠ЕАК = ЕСО (как соответственные элементы в равных треугольниках ΔАКВ и ΔСКD)
- Вертикальные углы равны.
⇒ ∠КЕА = ∠ОЕС (вертикальные)
- Сумма углов треугольника равна 180°.
Если в треугольниках есть по два равных угла, то равны и третьи углы.
∠АКС = 90°
⇒ ∠АКС = ∠СОЕ = 90°
⇒ AB ⊥ CD
#SPJ1
Приложения:
Новые вопросы
Английский язык,
9 месяцев назад
Другие предметы,
9 месяцев назад
Английский язык,
9 месяцев назад
Биология,
9 месяцев назад
Қазақ тiлi,
6 лет назад
Математика,
6 лет назад