Докажите неравенство d^3+1≥d^2+d при d≥-1
Ответы на вопрос
Ответил Лотарингская
0
d^3+1≥d^2+d
d^3-d^2-d+1≥0
d^2(d-1)-(d-1)≥0
(d^2-1)(d-1)≥0
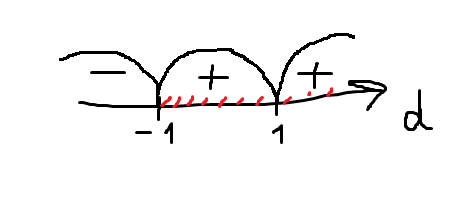
(d+1)*(d-1)^2≥0
d≥-1, т.е. получили, что неравенство верно при любом d≥-1
d^3-d^2-d+1≥0
d^2(d-1)-(d-1)≥0
(d^2-1)(d-1)≥0
(d+1)*(d-1)^2≥0
d≥-1, т.е. получили, что неравенство верно при любом d≥-1
Приложения:
Новые вопросы
Математика,
2 года назад
История,
2 года назад
Геометрия,
10 лет назад
Алгебра,
10 лет назад
История,
10 лет назад