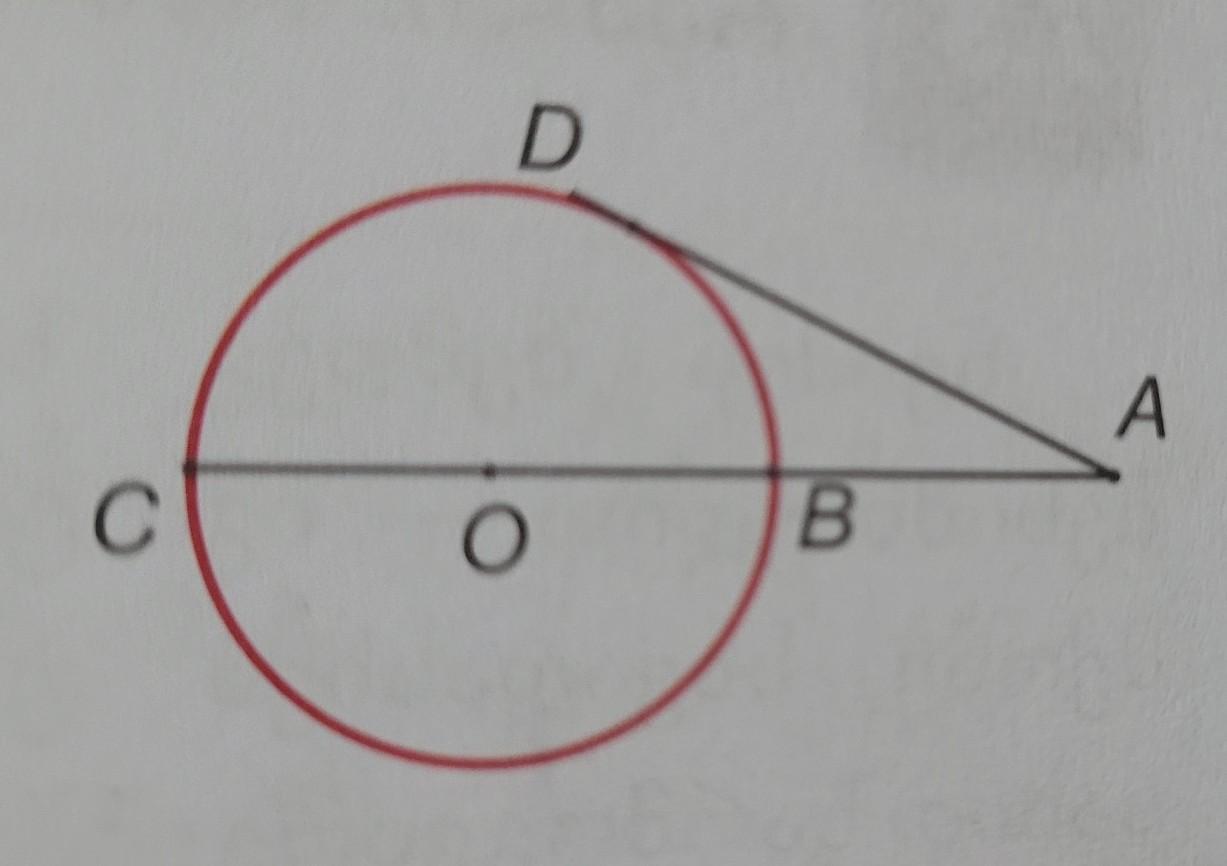
Длина сторон AD, проходящих от точки А до окружности, равна 24 см, а длина отрезка АС, проходящего через центр, равна 36 см. Найдите радиус окружности.
Приложения:
Ответы на вопрос
Ответил markus86
0
Пусть радиус окружности равен r. Тогда, по теореме Пифагора, получаем:
AC^2=AD^2+CD^2 \Rightarrow 36^2=r^2+12^2 \Rightarrow r^2=36^2-12^2=1200
Ответ: радиус окружности равен $\sqrt{1200}=20\sqrt{3}$ см.
AC^2=AD^2+CD^2 \Rightarrow 36^2=r^2+12^2 \Rightarrow r^2=36^2-12^2=1200
Ответ: радиус окружности равен $\sqrt{1200}=20\sqrt{3}$ см.
anavasileva14042008:
но в ответе написано 10см
Новые вопросы