Question

Даю 40 баллов. Геометрия.

Answer 1

Решение:
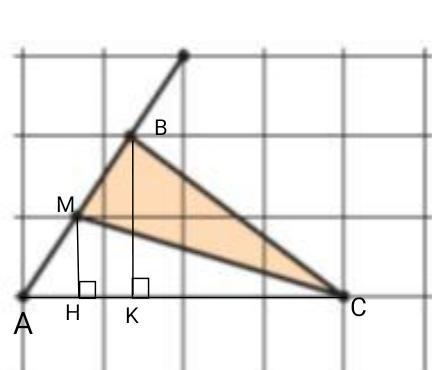
№29)
S(∆ABC)=AC*BK/2=4*2/2=4 кл.
S(∆MBC)=S(∆ABC)/2=4/2=2 кл.
Ответ: 2клетки.

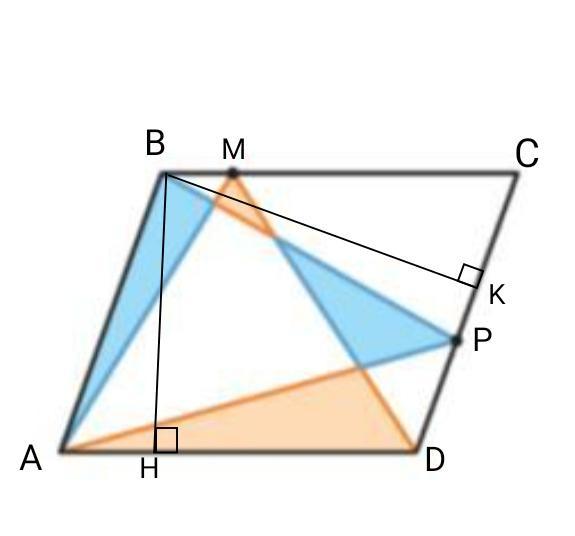
№28)
Опустим высоты параллелограма ВН и ВК.
S(ABCD)=BH*AD;
S(ABCD)=BK*DC;.

Рассмотрим треугольник ∆АМD.
Высота треугольника является ВН на сторону АD.
S(∆AMD)=BH*AD/2; т.е. площадь треугольника ∆АМD, равна половине площади параллелограма ABCD.
S(∆AMD)=S(ABCD)/2.

Рассмотрим треугольник ∆АВР.
Высота треугольника является ВК т.к. стороны параллелограма АВ=СD. то можно записать площадь треугольника
S(∆ABP)=BK*DC/2, площадь треугольника ∆АВР, равна половине площади параллелограма ABCD.
S(∆ABP)=S(ABCD)/2.

Треугольник ∆АВР равновеликий треугольнику ∆АМD.
S(∆ABP)=S(∆AMD).
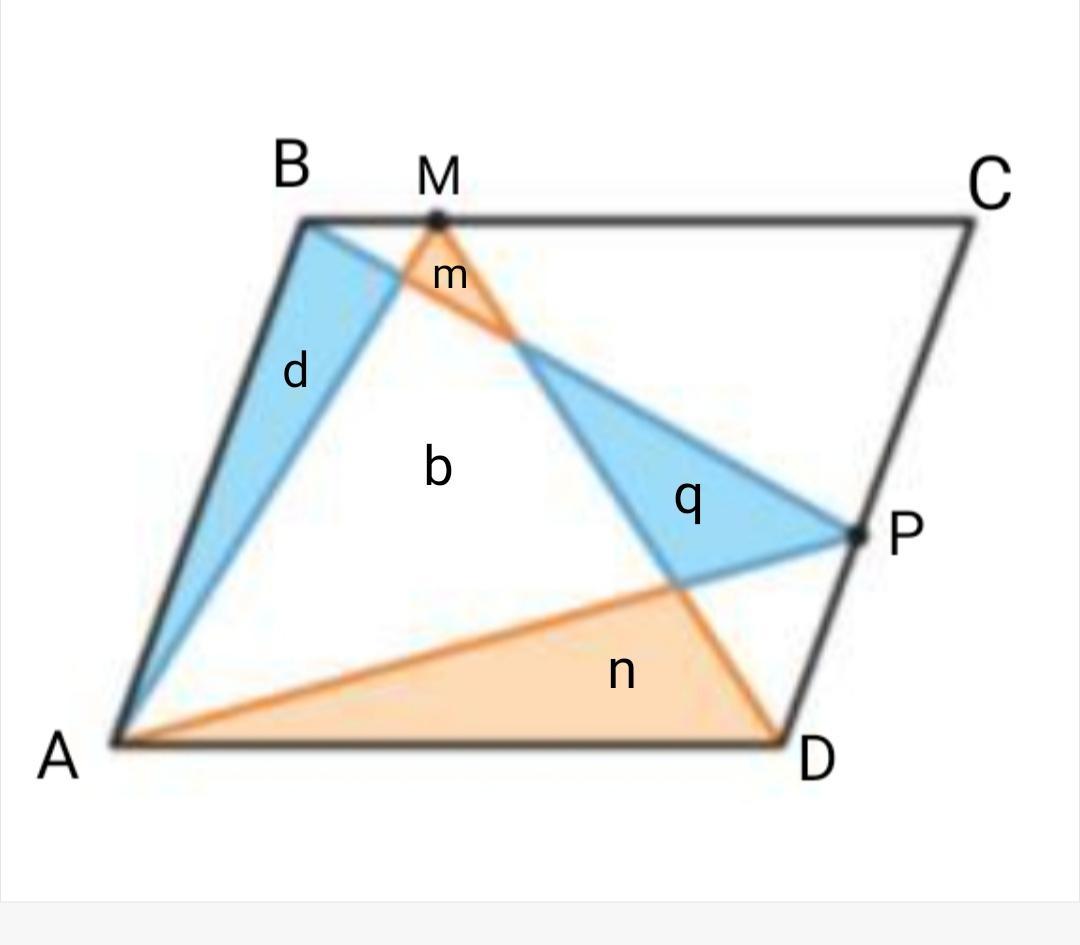
Разделим площади треугольников на части, и отметим каждую площадь буквой.
Так S(∆ABP)=d+b+q.
А площадь треугольника S(∆AMD)=m+b+n.
Так как треугольники равновеликие, приравниваем.
d+b+q=m+b+n.
b- в правой и левой части сокращаем.
Получили d+q=m+n.
Сумма площадей оранжевых треугольников равна сумме площадей голубых треугольников.
Что и требовалось доказать.