Даны координаты точек А (0;-1;2), В (-1;4;3), С (-2;1;0) и Д (-1;0;3). Вычислить координаты вектора р=ВА+СД. Вычислить длину вектора АС.
Ответы на вопрос
Ответил Andr1806
0
Координаты вектора равны разности соответствующих координат точек его конца и начала ab{х2-х1;y2-y1;z2-z1}
Сложение векторов : a+b=(x1+x2;y1+y2;z1+z2).
Вектор ВА{0-(-1);-1-4;2-3} или BA{1;-5;-1}.
Вектор CD{-1-2;0-1;3-0} или CD{-3;-1;3}.
Вектор р{1+(-3);-5+(-1);-1+3} или p{-2;-6;2}.
Длина (модуль) вектора
|АС| = √[(Xc-Xa)²+(Yc-Ya)²+(Zc-Za)²] или |AC|=√(-2²+2²+-2²)=2√3.
Ответ: р{-2;-6;2}; |AC|=2√3.
Сложение векторов : a+b=(x1+x2;y1+y2;z1+z2).
Вектор ВА{0-(-1);-1-4;2-3} или BA{1;-5;-1}.
Вектор CD{-1-2;0-1;3-0} или CD{-3;-1;3}.
Вектор р{1+(-3);-5+(-1);-1+3} или p{-2;-6;2}.
Длина (модуль) вектора
|АС| = √[(Xc-Xa)²+(Yc-Ya)²+(Zc-Za)²] или |AC|=√(-2²+2²+-2²)=2√3.
Ответ: р{-2;-6;2}; |AC|=2√3.
Ответил amin07am
0
Ответ ответ ответ ответ ответ
Приложения:
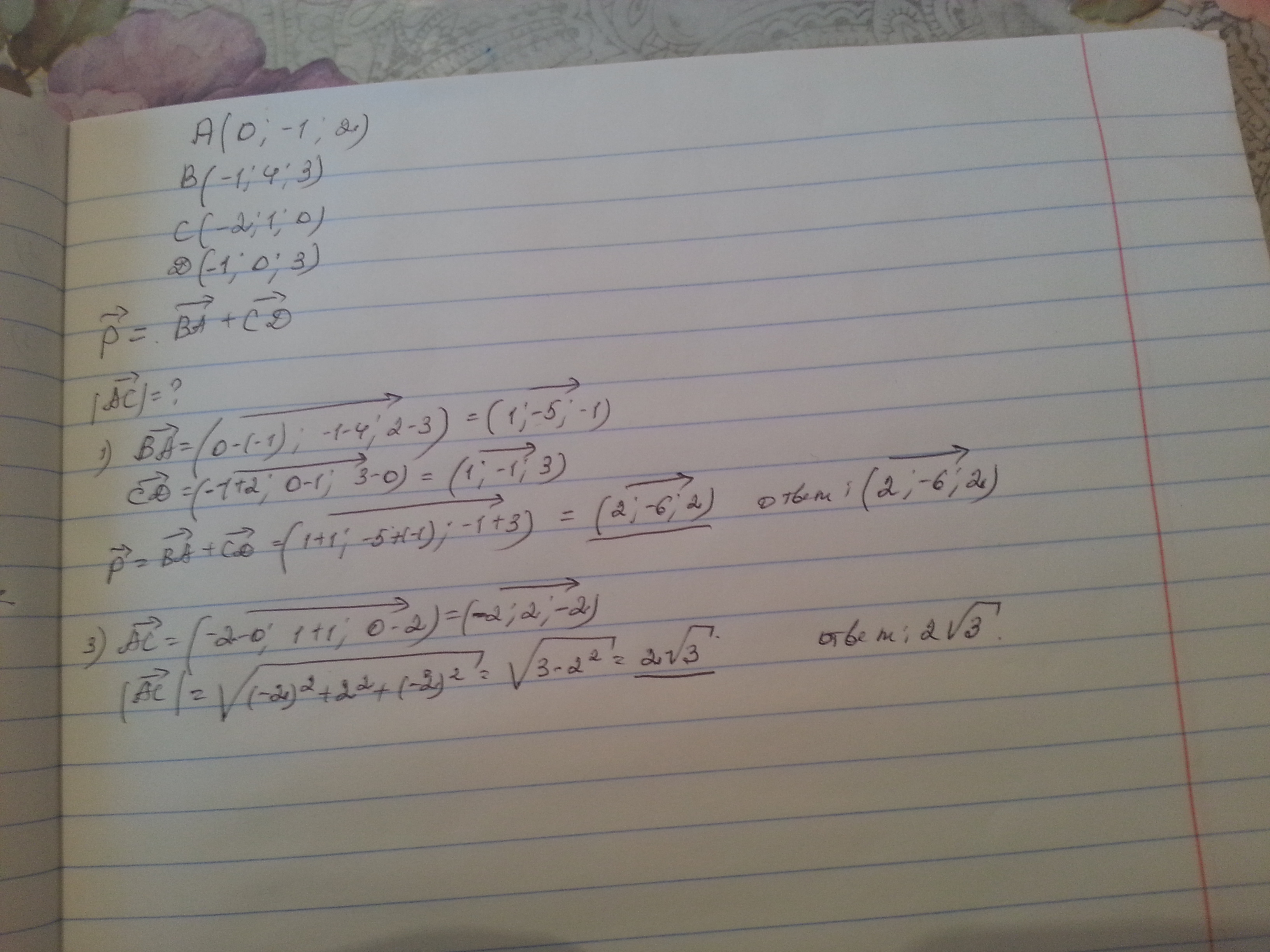
Новые вопросы
Другие предметы,
2 года назад
Математика,
2 года назад
Химия,
8 лет назад
Физика,
8 лет назад
Математика,
9 лет назад
Математика,
9 лет назад