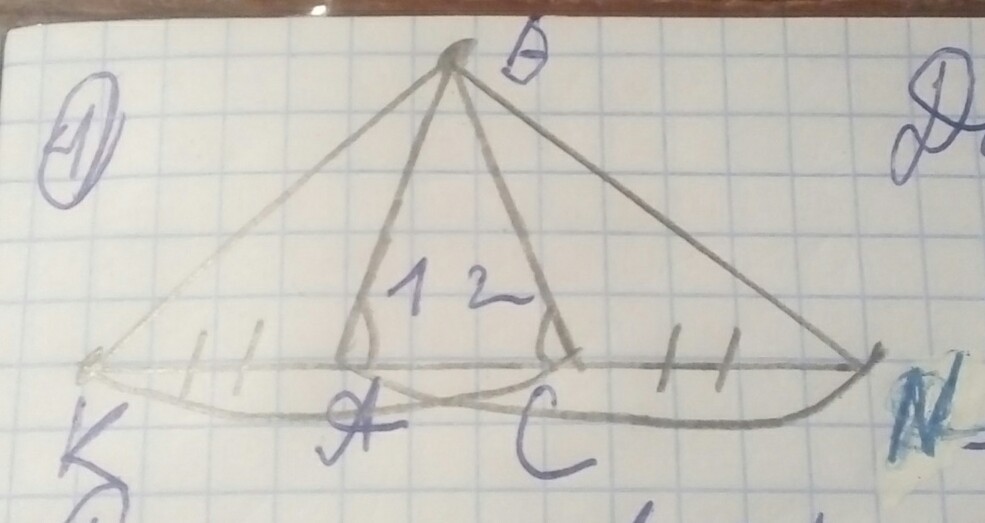
Дано: треугольник КСВ и треугольник NАВ
угол 1=угол 2; КА=СN
Доказать: треугольник КСВ=треугольник NAB; треугольник KAB=треугольник СNB.
Приложения:
Ответы на вопрос
Ответил Senus
0
Рассмотрим треугольники KCB и NAB, в них:
1)KA=NC(по условию)
2)AC=CB(т.к треугольник ABC - равнобдренны, потому что угол BAC = BCA)
3)Угол KAB = NCB(тут по разному можно, но я думаю что они являются смежными, а по условию 1 и 2 угол, равны)
1)KA=NC(по условию)
2)AC=CB(т.к треугольник ABC - равнобдренны, потому что угол BAC = BCA)
3)Угол KAB = NCB(тут по разному можно, но я думаю что они являются смежными, а по условию 1 и 2 угол, равны)
Ответил Безумная1111
0
спасибо поможешь ещё с если доказать КАС и СNB
Ответил Senus
0
Сторона KC = KA+AC, а NA = NC+AC => AC- общее, KA=NC(по условию)
Ответил Безумная1111
0
Спасибо.
Ответил Senus
0
без проблем!
Новые вопросы
Геометрия,
2 года назад
Українська мова,
2 года назад
Алгебра,
8 лет назад
Алгебра,
8 лет назад
Математика,
9 лет назад