Question

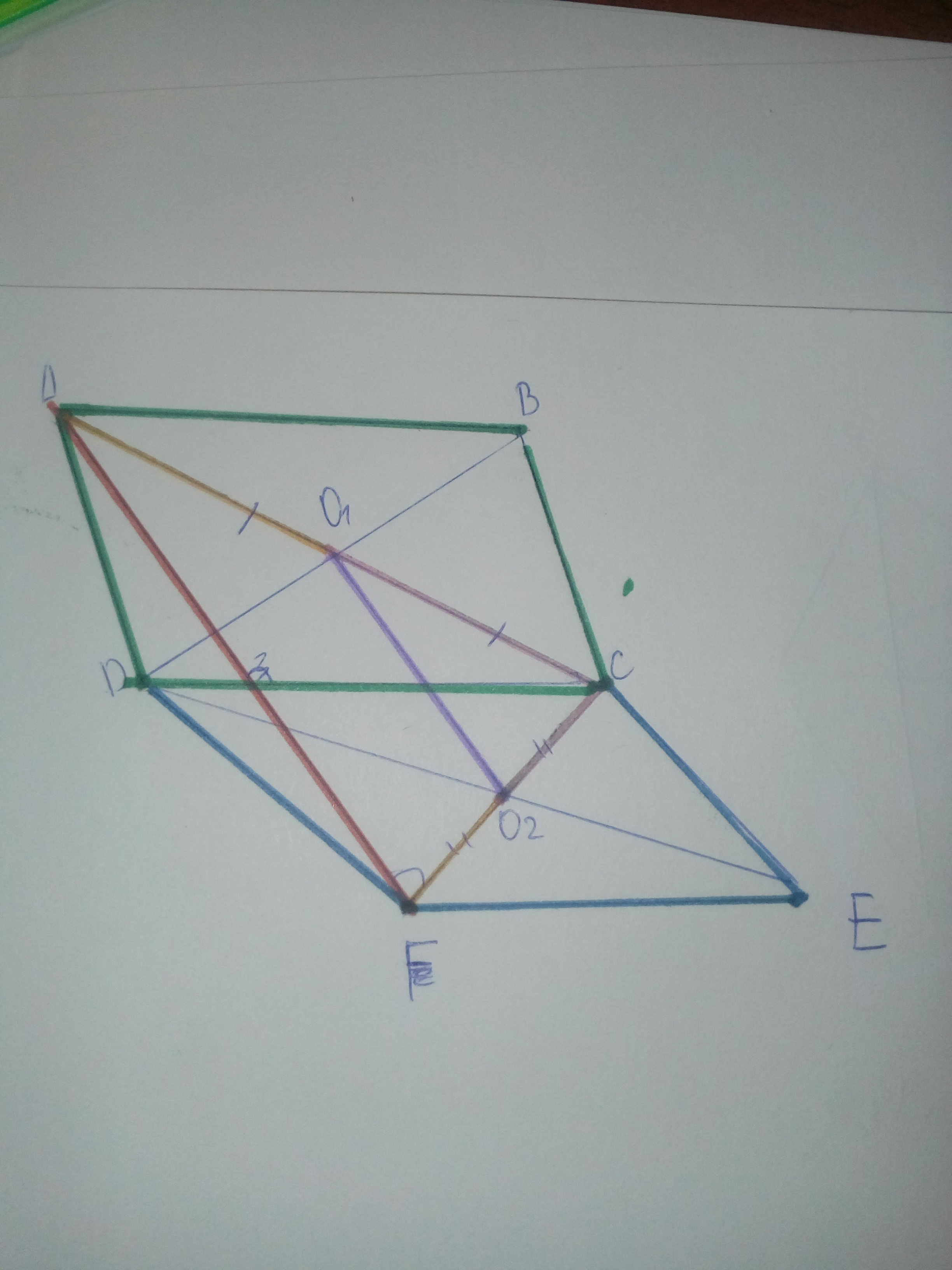
четырехугольники ABCD И DCEF ИМЕЮТ ОБЩУЮ СТОРОНУ CD. A, D F НЕ ЛЕЖАТ НА ОДНОЙ ПРЯМОЙ AB=CD=EF AB││CD││EF дИАГОНАЛИ ЧЕТЫРЕХУГОЛЬНИКОВ ABCD И DCEF ПЕРЕСЕКАЮТСЯ СООТВЕТСТВЕННО В ТОЧКАХ О1 И И О2 . ДОКАЖИТЕ ЧТО AF ││O1O2 И AF=2*O1*O2

Answer 1

Т.к. AB = DC и AB || DC, то ABCD - параллелограмм.
Аналогично т.к. DC || EF и DC = EF, то DCEF - параллелограмм.
По свойству диагоналей параллелограмма:
AO1 = O1C и аналогично FO2 = O2C.
Рассмотрим ∆АСF.
AO1 = O1C и FO2 = O2C. Тогда O1O2 - средняя линия ∆ACF.
Тогда O1O2 = 1/2AF или AF = 2O1O2 и O1O2 || AF.