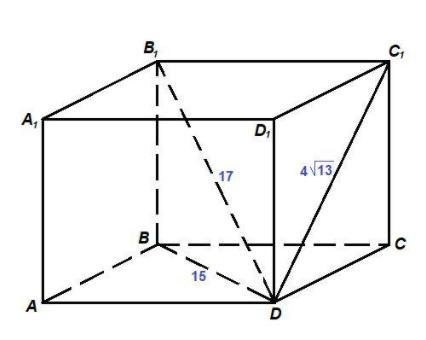
50 баллов! Найдите объем прямоугольного параллелепипеда ABCDA1B1C1D1 , если B1D=17, AC=15, A1D=12, необходим рисунок
Ответы на вопрос
Ответил raisatmazakova40
1
Ответ:
864 см³
Объяснение:
Все грани прямоугольного параллелепипеда - прямоугольники, диагонали прямоугольника равны, поэтому
АС = BD = 15 см
Объем прямоугольного параллелепипеда равен произведению трех его измерений. Найдем их.
ΔВ₁BD: ∠B₁BD = 90°, по теореме Пифагора:
ВВ₁ = √(DB₁² - BD²) = √(17² - 15²) = √((17 - 15)(17 + 15)) =
= √(2 · 32) = 64 = 8 см
СС₁ = ВВ₁ = 8 см
ΔDCC₁: ∠DCC₁ = 90°, по теореме Пифагора:
CD = √(DC₁² - CC₁²) = √((4√13)² - 8²) = √(208 - 64) = √144 = 12 см
ΔBCD: ∠BCD = 90°, по теореме Пифагора:
BC = √(BD² - CD²) = √(15² - 12²) = √((15 - 12)(15 + 12)) =
= √(3 · 27) = √81 = 9 см
V = CD · BC · BB₁ = 12 · 9 · 8 = 864 см³
Приложения:
2hfkk6nwqg:
Не верно!
Новые вопросы