Question

10 класс 50 баллов
Розв’яжіть задачу:

Answer 1

Ответ:

Отрезок CD равен 8√2 см.

Объяснение:

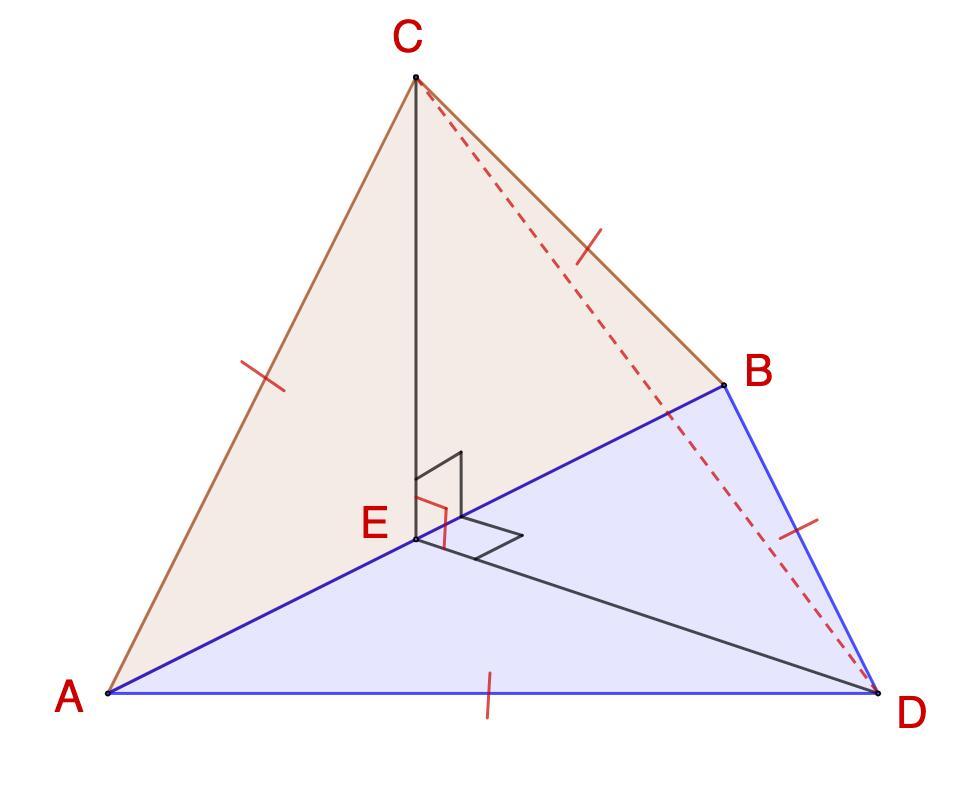
6. Два равнобедренные прямоугольные треугольники ABC и ABD лежат в перпендикулярных плоскостях и имеют общую гипотенузу АВ. Найдите CD, если AB = 16 см.

Дано: (АВС) ⊥ (ABD)

ΔABC и ΔABD - прямоугольные, равнобедренные;

АВ = 16 см - гипотенуза.

Найти: CD

Решение:

Проведем высоту СЕ, соединим Е и D.

1. Рассмотрим ΔABC - прямоугольный, равнобедренный.

• Сумма острых углов прямоугольного треугольника равна 90°.

⇒ ∠САВ + ∠СВА = 90°

• Углы при основании равнобедренного треугольника равны.

⇒ ∠САВ = ∠СВА = 90° : 2 = 45°

СЕ - высота (построение)

• В равнобедренном треугольнике высота, проведенная к основанию, является медианой.

⇒ АЕ = ЕВ = 16 : 2 = 8 (см)

2. Рассмотрим ΔАСЕ - прямоугольный.

• Тангенс угла - отношение противолежащего катета к прилежащему.

$\displaystyle tg\;45^0=\frac{CE}{AE} \\\\1=\frac{CE}{8}\;\;\;\;\;\Rightarrow \;\;\;\;\;CE = 8$   (см)

3. Рассмотрим ΔABD - равнобедренный, прямоугольный.

DE - медиана, высота.

Аналогично пункту 1, DE = 8 см.

4. Рассмотрим ΔECD.

• Свойство перпендикулярных плоскостей:
• Если прямая лежит в одной из двух взаимно перпендикулярных плоскостей и перпендикулярна линии их пересечения, то эта прямая перпендикулярна второй плоскости.

⇒ CE ⊥ ABD

• Если прямая перпендикулярна плоскости, то она перпендикулярна любой прямой, принадлежащей этой плоскости.

⇒ СЕ ⊥ ED.

⇒ ΔECD - прямоугольный.

По теореме Пифагора найдем CD:

CD² = EC² + ED² = 64 + 64 = 128   ⇒   CD = 8√2 (см)