Question

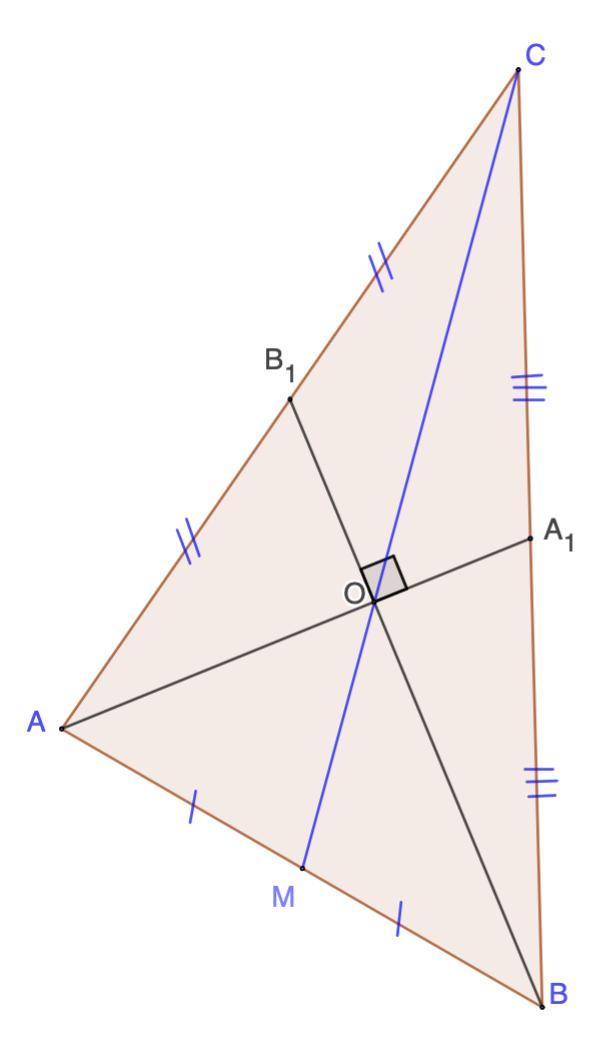
1.186. Медианы АА, и ВВ, треугольника АВС пе- ресекаются в точке О под прямым углом (рис. 1.84). Докажите, что выполняется равенство АВ = СO.​

Answer 1

Ответ:

Доказано, что выполняется равенство АВ = СO.​

Объяснение:

1.186. Медианы АА₁, и ВВ₁, треугольника АВС пересекаются в точке О под прямым углом (рис. 1.84). Докажите, что выполняется равенство АВ = СO.​

Дано: ΔАВС.

АА₁, ⊥ ВВ₁;  АА₁ ∩ ВВ₁ = О - медианы.

Доказать: АВ = СO

Доказательство:

• Проведем отрезок СМ.

• Медианы треугольника пересекаются в одной точке и делятся этой точкой в отношении 2 : 1, считая от вершины.

⇒  СМ - медиана.

СО = 2 МО

Рассмотрим ΔАОВ - прямоугольный.

АМ = МВ (СМ - медиана ΔАВС)  ⇒   ОМ - медиана ΔАОВ.

• Медиана, проведенная из вершины прямого угла к гипотенузе равна половине гипотенузы.

⇒ АВ = 2 МО

СО = 2 МО;   АВ = 2 МО

⇒ СО = АВ

#SPJ1